AIで解く最適化問題　～今日から使える深層強化学習～

2019新卒入社の東川です。この記事ではシャッフルランチという社内交流企画で現れた最適化問題に対して、強化学習を適用した事例についてご紹介します。

シャッフルランチとは

フォルシアで行っているシャッフルランチとは業務上の関わりの薄い社員同士のコミュニケーション促進のために月一回開催している社内企画であり、Slackの特定のチャンネルにjoinした参加希望者を自動的に3-4人のグループに分けて、それらのグループでランチに行くというものです。シャッフルランチの費用は会社が負担しています。
（開催の背景についてはこちらの記事、技術的側面についてはこちらの記事をご覧ください）

幸い社内でも好評であり、毎月60人強の社員が継続して参加しています。

フォルシアのシャッフルランチの特徴は、グループ分けが完全にランダムではなく、参加者間の会社での関わりができるだけ小さくなるようにグループ分けされているという点です。これにはできるだけ普段の業務で関わりのない人と交流してほしいという運営側の意図があります。参加者間の「会社での関わり」の指標としては「Slackの共通で加入しているチャンネルの数」を使用しており、これを親密度と呼ぶことにします。会社での関わりが薄い2人の社員は共通で加入しているSlackチャンネルの数も少ないと考えられるためです。

組み合わせ最適化としてのシャッフルランチ

シャッフルランチを最適化問題として定義するには何らかの指標が必要です。グループ内のコストをグループに属する2者間の親密度の合計とし、グループ分けのコストを、全グループのグループ内のコストの総和として定義します。このコストが最小化されるとき、会社での関わりができるだけ小さくなるようなグループ分けになっているはずです。

わかりやすい例として、人を3人ずつのグループへ分割して考えましょう（図1）。

まず、2者間の関係性を点数化し、図1(a)のような図を作成します。続いて、図1(b)のような3人ずつのグループ分けを考えます。この時「グループ内のコスト」はそれぞれ5+3+5(=13), 8+1+5(=14)であり、「グループ分けのコスト」は13+14=27です。図1(c)の「グループ分けのコスト」は70であり、図1(b)のグループ分けは図1(c)のグループ分けに比べて、参加者間の会社での関わりが小さいグループ分けになっているということができます。

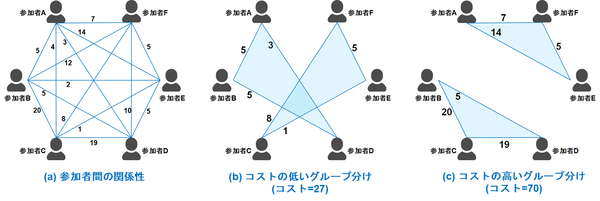
図1: 6人組を3人+3人のグループに分割する場合。数字は2者間の共通のチャンネルの数を表します。
図(b)の「グループ分けのコスト」は27で、図(c)の「グループ分けのコスト」は70です。

シャッフルランチの組み分けにおいて会社での関わりができるだけ小さい組み分けを探し出すことは重要であり、実際アンケートを見ると「普段関わりのない人と話す機会ができてよかった」という声がたくさんあります。一方で、上記の設定にしたがって「グループ分けのコスト」を最小にするグループ分けを求めるのは、以下の2つの観点から難しい問題です。

• 考えうる組み合わせが膨大である
  上の6人を分ける問題ではグループ分けの数は 6!/(3!×3!)=20 通りで全探索が可能です。一方、この組み合わせの数は全体の人数とともに爆発的に増えます。例えば、60人を4人ずつのグループに分ける場合の数は 60!/(415×15!)≒6×1060 通りあり、これを網羅的に調べるのは現実的ではありません。
• グループ分けのコストを最小化するのは難しい
  ある一つのグループ分けに対してグループ内のコストを最小化するのは簡単ですが、一つのグループ分けを最小に使用すると往々にして他のグループのコストが上がってしまうことがあります。
  グループ内のコストの最小化と全体のコストの最小化はトレードオフの関係にあり、ちょうど良いところを定量的に決めるのは難しい問題です。

上記2つの問題に対して、流行りの強化学習が適用できるのではないかと思い、実際に試してみました（あと私自身、強化学習に触れてみたかったという理由もあります）。

以下では、そのインストール方法とサンプルコードを中心に説明します。深層学習や強化学習のライブラリやフレームワークを使用するのは私にとって今回が初めてでしたが、そのインストールの簡便さとコーディングのインターフェースの簡単さには感銘を受けました。

この記事が、組み合わせ最適化問題をできるだけ手軽に解きたい、深層強化学習のライブラリに触れてみたいという方の一助になれば幸いです。

強化学習とは？強化学習に必要な各種フレームワークとライブラリのインストール

強化学習とは近年流行している機械学習の一つの分野であり、GoogleのAlpha Goでも使用されている技術として一躍注目を集めました。機械学習には大まかに教師あり学習、教師なし学習、強化学習の3つの分野があります。

• 教師あり学習：多数の教師データを基に入出力の関係を学習するものです。画像分類などに使用されます。
• 教師なし学習：多数のデータを基にデータのカテゴライズを学習するものです。クラスタリングなどに使用されます。
• 強化学習：多数の試行錯誤を基に最適な戦略を選び出し、「価値」を最適化するものです。

教師なし学習や教師あり学習では多数のデータが必要ですが、強化学習では必要ありません。多数回の試行錯誤を通してデータが作成され、それを基に自律的に学習が進むからです。
強化学習の最適戦略の探索において、AIの核となる技術である深層学習が使用されており、しばしば深層強化学習と呼ばれることもあります。以下では深層強化学習の中でもQ学習、とそこで用いられる手法であるDQN(Deep Q Network)にフォーカスして解説します。

強化学習の問題設定

強化学習では、エージェントとエージェントが制御する対象である環境を考えます。強化学習で重要になる概念が選択action、状態state、観測データobservation、報酬rewardです(図2)。
エージェントは各ステップで何らかのactionを選択し環境のstateが変化します。環境は変化後のstateに対してobservationを計算し、observationとrewardを返却します。エージェントは多数の試行錯誤からactionとobservation, rewardの関係性を学習し、rewardを最大化するような最適戦略を導き出します。

今回の例では環境はグループ分けの全体であり、actionは例えば2つのグループの人を交換するという操作、observationは各グループの点数などです。rewardは現在のグループ分けのコストに-1をかけたものであり、rewardの最大化はグループ分けのコストの最小化と同値です。

一点注意するべき点はrewardを最大化する戦略に収束させるためには、取りうるactionの値(action_space)とstateの取りうる値の空間(observation_space)を適切に選ばなければいけないしないということです。人間の学習プロセスがそうであるように、可能なactionが著しく少なかったり、stateから抽出された値がrewardの最大化にあまり関係のないものだったりする場合、強化学習を通して上手い最適戦略が得られない場合もあります。

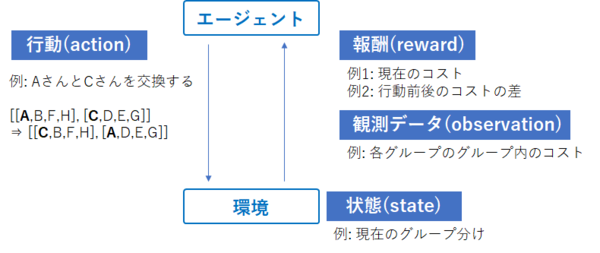
図2: 強化学習の基本概念。エージェントはactionに対するstateの挙動を見て、試行錯誤しながらrewardを最大化します。
例は今回のグループ分けの最適化において使用されたものを表します。

今回は強化学習ライブラリとしてkeras-rl+gymを使用しました。強化学習のフレームワークに触れるのは私にとって初めての経験でしたが、離散最適化問題のソルバーとして強化学習を用いることのメリットとして以下のような点を感じました。

• ライブラリの導入コストが低く、必要となるコーディングも少ない
• フレームワークにしたがって、直感的に書くことができる
• デバッグツールと可視化ツールが豊富で開発がしやすい

tensorflow, keras, keras-rl, gymのインストール

kerasとはPythonで書かれたニューラルネットワークライブラリであり、その使いやすさから深層学習の研究と実践で広く使用されています。今回はバックエンドとしてtensorflowを使用するので、それもインストールします。インストールはpipを使って以下のコマンドで出来ます。

pip install tensorflow
pip install keras

深層強化学習をするために、さらにkeras-rlとOpenAI gymをインストールします。keras-rlとはkerasを利用してDQNなどの深層強化学習を実装できるライブラリであり、gymは強化学習に必要な一連の変数を定義するために必要なライブラリです。下で見るように上述のaction, stateなどの枠組みはgymのクラスを継承することで作成できます。

git clone https://github.com/matthiasplappert/keras-rl.git
pip install ./keras-rl
pip install gym

強化学習による最適なグループ分けの探索

問題設定と強化学習の環境との対応

nm 人を ng 人ずつのグループに分けることを考えます。すべてのメンバーにインデックス i(=1,2,...nm)を貼ります。各グループ分けを表現するために長さnmの配列Gを考え、i番目の人がグループG[ i]に属しているとします。

例えば、G[3]=1であれば3番目のメンバーはグループ1に所属しているという形です(図3(a))。iとメンバーjの親密度をR[i,j]として、これを行列要素に持つようなnm×nm行列Rを定義し、これを親密度行列と呼ぶことにします(図3(b))。この時、グループ分けGに対してg番目のグループのコストとグループ分け全体のコストはそれぞれ図3(c), (d)のように表現されます。

図3: グループ分けGと親密度行列R、コストCの説明。
χは定義関数でχ(true)=1,χ(false)=0です。

今回の問題と強化学習の変数との対応は下表の通りです。stateはグループ分けG、rewardは−Cです。actionはGから新しいグループ分けG′を生成する操作であり、例えばメンバーの入れ替えなどであり、observationは例えば現在のグループからメンバーの入れ替えをした時の点数の変化などをとります。

state	グループ分けG(図3(a))、例: [0,2,1,2,0,1]( 6人を3グループに分ける場合)
action	新しいグループ分けG′を作る操作、例: メンバー2と3の入れ替えG=[0,1,2,2,0,1]⇒G′=[0,2,1,2,0,1]
observation	例: 各グループの点数
reward	グループ分けのコストに−1をかけたもの (−C) (図3(d))

表1: 強化学習の変数state, action, observation, rewardと今回の問題との対応

学習環境の定義

最適化の環境を表すクラス（下ではGroupingEnvとしています）はgymのクラスcore.Envを継承して作成します。

class GroupingEnv(gym.core.Env):
    # クラスの定義

core.Envを継承するには5つのメソッドstep, reset, render, close, seedと3つのプロパティaction_space, observation_space, reward_spaceを実装する必要があります。

• step: 各ステップで実行される関数です。actionを引数に取り、observation, reward, is_done（終了条件を満たしたかどうか）, infoを出力します。今回のケースでは、actionの値にしたがってメンバーを入れ替える⇒メソッドget_observationで入れ替え後の状態に対して観測データを得る⇒メソッドget_rewardで報酬を計算する⇒終了条件を満たしているかを判定する、の4ステップを入れました。

    # 各ステップで実行される操作
    def step(self, action):
        self.time += 1
        # step1: actionに戻づいてグループ分けを更新する
        self.grouping = self.exchange_member(self.grouping, action).copy()
        # step2: 観測データ(observation)の計算
        observation = self.get_observation()
        # step3: 報酬(reward)の計算
        reward = self.get_reward(self.grouping)
        # step4: 終了時刻を満たしているかの判定
        done = self.check_is_done()
        info = {}
        return observation, reward, done, info

infoは必要なければ空ディレクトリにします。

• reset: 状態の初期化をする関数です。出力はstateから得られる観測データobservationとします。今回は以下のようにランダムなグループ分けに初期化するようにしました。

    def reset(self):
        # 変数の初期化。ランダムなグループ分けに初期化する
        self.time = 0
        self.grouping = self.get_random_grouping()
        return self.get_observation()

    # ランダムなグループ分けを得るための関数
    def get_random_grouping(self):
        grouping = list(range(self.n_group)) * int(self.n_member / self.n_group)
        random.shuffle(grouping)
        return grouping

• render, close, seed: render, close, seedはそれぞれ、環境の可視化、終了時の処理、乱数の固定を表す関数です。特に必要なければ、passとします。

def render(self, mode):
    # 画面への描画
    pass

• action_space: action_spaceとはactionの取りうる値の空間を指します。actionとして2人のメンバーの入れ替えを採用しているため、メンバーnm に対して、actionとしては nm×(nm−1)/2 通りの選択肢あります。これだとメンバー数の増加とともに学習のコストが増大してしまうため、今回は「可能なactionの集合に対してactionにしたがって組み替えたときのコストを計算し、コストの小さい10通りのうち何番目を選ぶか」という設定にしました（かなり経験的な方法に寄せています）。

        self.n_action = 10
        self.action_space = gym.spaces.Discrete(self.n_action) # actionの取りうる値

ここでgym.spaces.Discrete(N)はN個の離散値の空間を表します。

• observation_space: observation_spaceとは観測データの取りうる値の空間を表します。今回の場合、上記のコストが小さくなるような10通りのメンバーの入れ替えのコストを観測データとしました。

        self.observation_space = gym.spaces.Box(low=-10, high=10, shape=(self.n_action,)) # 観測データの取りうる値

必要に応じてstateからobservationを計算するための関数get_observation、rewardを計算するための関数get_reward、終了条件を満たしているかを判定する関数check_is_doneを定義します。
最後に学習の終了条件を定義します。今回は終了条件は単純に「ステップ数の上限(20回)を超えたら終了する」としました。

    # 終了条件を判定する関数
    def check_is_done(self):
        # 最大数に達したら終了する
        return self.time == self.max_step
    

出来上がったコード全体は以下の通りです。

import gym.spaces
import copy
import numpy as np
import random
class GroupingEnv(gym.core.Env):
    metadata = {'render.modes': ['human', 'rgb_array']}
    def __init__(self, relationship_matrix, n_group, n_member):
        self.relationship_matrix = relationship_matrix # 2者間の関係性を表す行列
        self.n_member = n_member # 全体のメンバー数
        self.n_group = n_group # グループの数
        self.grouping = list(range(self.n_group)) * int(self.n_member / self.n_group) # グループ分け
        self.group_id_list = list(range(n_group)) # groupのidのリスト
        self.n_action = 10
        self.action_space = gym.spaces.Discrete(self.n_action) # actionの取りうる値
        self.observation_space = gym.spaces.Box(low=-10, high=10, shape=(self.n_action,)) # 観測データの取りうる値
        self.time = 0 # ステップ
        self.max_step = 20 # ステップの最大数
        self.pair_list = self.get_pair_list()
        self.candidate_list = []

    # 各ステップで実行される操作
    def step(self, action):
        self.time += 1
        # step1: actionに戻づいてグループ分けを更新する
        self.grouping = self.exchange_member_action(self.grouping, action).copy()
        # step2: 観測データ(observation)の計算
        observation = self.get_observation()
        # step3: 報酬(reward)の計算
        reward = self.get_reward(self.grouping)
        # step4: 終了時刻を満たしているかの判定
        done = self.check_is_done()
        info = {}
        return observation, reward, done, info
    
    def reset(self):
        # 変数の初期化。ランダムなグループ分けに初期化する
        self.time = 0
        self.grouping = self.get_random_grouping()
        return self.get_observation()
    
    def render(self, mode):
        # 画面への描画
        pass
    
    def close(self):
        # 終了時の処理
        pass
    
    def seed(self):
        # 乱数の固定
        pass
    
    # 報酬を計算する関数
    def get_reward(self, grouping):
        return -1 * self.total_grouping_cost(grouping) # 報酬 = グループ分けgroupingのコスト*(-1)
    
    # 観測データを計算する関数
    def get_observation(self):
        grouping = self.grouping.copy()
        candidate_list = []
        for pair in self.pair_list:
            id1, id2 = pair
            cost = self.get_reward(self.exchange_member_pair(grouping, id1, id2))
            candidate_list.append([id1, id2, cost])
        
        self.candidate_list = sorted(candidate_list, key=lambda x:-x[2])[0:self.n_action]
        return [cand[2] for cand in self.candidate_list]
    
    # 終了条件を判定する関数
    def check_is_done(self):
        # 最大数に達したら終了する
        return self.time == self.max_step
    
    # actionの値に応じて、2人のグループを交換する関数
    def exchange_member_action(self, grouping, action):
        new_grouping = grouping.copy()
        id1, id2, cost = self.candidate_list[action]
        new_grouping[id1] = grouping[id2] # id1のメンバーとid2のメンバーを交換
        new_grouping[id2] = grouping[id1]
        return new_grouping
    
    # id1, id2のメンバーを交換する関数
    def exchange_member_pair(self, grouping, id1, id2):
        new_grouping = grouping.copy()
        new_grouping[id1] = grouping[id2]
        new_grouping[id2] = grouping[id1]
        return new_grouping

    # ランダムなグループ分けを得るための関数
    def get_random_grouping(self):
        grouping = list(range(self.n_group)) * int(self.n_member / self.n_group)
        random.shuffle(grouping)
        return grouping
    
    # グループ分けのコストを計算する関数
    def total_grouping_cost(self, grouping):
        return sum([self.group_cost(grouping, group_id) for group_id in self.group_id_list])
    
    # グループgroup_idのコストの計算
    def group_cost(self, grouping, group_id):
        group = [i for i, _x in enumerate(grouping) if _x == group_id]
        n_pair = len(group) * (len(group) - 1)
        return self.relationship_matrix[np.ix_(group, group)].flatten().sum() / n_pair
    
    # 可能なペアの列挙
    def get_pair_list(self):
        pair_list = []
        for id1 in list(range(self.n_member)):
            for id2 in list(range(self.n_member)):
                if id1 < id2:
                    pair_list.append([id1, id2])
        return pair_list

定義された環境を使って学習環境を定義します。例えば20人を4つのグループに分割する問題を考えるときは以下のようにします（親密度行列Rは本来Slackから取得される情報を使って定義されるべきですが、今回は簡単のため乱数を要素とする行列としました）。

# 組み分けの環境の定義
n_member = 20
n_group = 4
n_action = 10

# 親密度行列の定義
# NOTE: ランダム行列で代用
relationship_matrix = np.array([random.random() for _ in range(n_member ** 2)]).reshape(n_member, n_member)
env = GroupingEnv(relationship_matrix, n_group, n_member)

ニューラルネットワークの定義と訓練

続いて、この環境に最適な行動を求めるためのモデルをニューラルネットワークで求めます。

from keras.models import Sequential
from keras.layers import Dense, Activation, Flatten
from keras.optimizers import Adam
from rl.agents.dqn import DQNAgent
from rl.policy import BoltzmannQPolicy
from rl.memory import SequentialMemory

# ニューラルネットワークの構造を定義
model = Sequential()
model.add(Flatten(input_shape=(1,) + env.observation_space.shape))
model.add(Dense(128))
model.add(Activation('relu'))
model.add(Dense(n_action))
model.add(Activation('linear'))
print(model.summary()) # モデルの定義をコンソールに出力

# モデルのコンパイル
memory = SequentialMemory(limit=50000, window_length=1)
policy = BoltzmannQPolicy(tau=1.)
dqn = DQNAgent(model=model, nb_actions=n_action, memory=memory, nb_steps_warmup=50, target_model_update=1e-2, policy=policy)
dqn.compile(Adam(lr=1e-3), metrics=['mae'])

ニューラルネットワークの中間層は1個としました。

モデルの訓練は以下の通りです。

# 訓練
history = dqn.fit(env, nb_steps=5000, visualize=False, verbose=2, nb_max_episode_steps=300)

訓練中は以下のようなレコードが出て、rewardやmean_qの推移が表示されます。
mean_qは学習の進み具合を表すパラメータであり、これの収束は学習が終了したことを表します。

  200/5000: episode: 1, duration: 2.922s, episode steps: 200, steps per second: 68, episode reward: -298.082, mean reward: -1.490 [-1.593, -1.376], mean action: 31.190 [0.000, 63.000], mean observation: 0.547 [0.000, 1.000], loss: 0.052949, mae: 1.083208, mean_q: -0.088404
  400/5000: episode: 2, duration: 1.784s, episode steps: 200, steps per second: 112, episode reward: -298.902, mean reward: -1.495 [-1.593, -1.376], mean action: 31.120 [0.000, 63.000], mean observation: 0.547 [0.000, 1.000], loss: 0.011003, mae: 2.727983, mean_q: -2.161458
  600/5000: episode: 3, duration: 1.781s, episode steps: 200, steps per second: 112, episode reward: -298.719, mean reward: -1.494 [-1.590, -1.388], mean action: 32.490 [0.000, 63.000], mean observation: 0.547 [0.000, 1.000], loss: 0.048550, mae: 4.750234, mean_q: -3.986667

最後に評価をします。ログを記録するために、rl.callbacks.Callbackを拡張したクラスEpisodeLoggerを作成し、dqn.testのコールバックとして渡します。このように簡単に学習過程のログが作れることもkeras-rlの魅力の一つです。

import rl.callbacks

# ログを記録するためのクラスの定義
class EpisodeLogger(rl.callbacks.Callback):
    def __init__(self):
        self.rewards = {}
    def on_episode_begin(self, episode, logs):
        self.rewards[episode] = []
    def on_step_end(self, step, logs):
        episode = logs['episode']
        self.rewards[episode].append(logs['reward'])

episode_logger = EpisodeLogger()
nb_episodes = 100
dqn.test(env, nb_episodes=nb_episodes, visualize=False, callbacks=[episode_logger])

テスト中は以下のようなレコードが出て、各エピソードの終了時点でのrewardが出力されます。

Testing for 100 episodes ...
Episode 1: reward: -60.495, steps: 20
Episode 2: reward: -61.666, steps: 20
Episode 3: reward: -59.772, steps: 20

上では100個のランダムなグループ分けを初期値として、最適化をしています。ステップごとのrewardの平均は図4左のように推移し、ステップとともにrewardが増加（すなわちグループ分けのコストCが減少）していることがわかります。

random_sampling = [env.get_reward(env.get_random_grouping()) for _ in list(range(10000))]

import matplotlib.pyplot as plt

plt.plot(mean_reward_list, label='N={}'.format(nb_episodes))
plt.xlabel('step', fontsize=18)
plt.ylabel('mean reward', fontsize=18)
plt.legend(loc='upper right', fontsize=18)
plt.show()
# plt.savefig('mean_award.png')

図4右は各エピソード終了時点でのrewardの頻度分布です。青のヒストグラムはN=10000でランダムにグループ分けを生成したときの頻度分布であり、強化学習を用いた最適化の方法のほうが系統的に良い結果を与えていることがわかります。

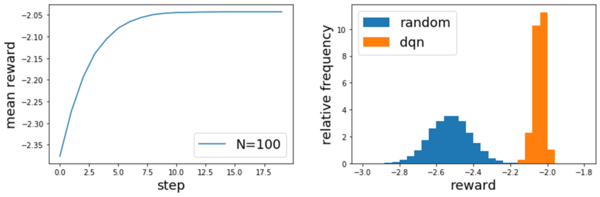
図4: (左)ステップ数に対するrewardの推移（100回平均）。
(右)エピソード終了時点でのrewardの値のランダムサンプリングとの比較

最後に

この記事ではシャッフルランチで出てきた離散最適化問題を例にして、強化学習により離散最適化問題の解法について紹介しました。今回実装してみて、組み合わせ最適化問題のソルバーに強化学習のフレームワークを使用することにはいくつかのメリットがあると感じました。

• 手軽。ライブラリをインストールして、動くものを作るまでそこまで時間がかからない
• action, reward, step, resetなどライブラリで使用されている用語が直感的で実装しやすい

組み合わせ最適化問題には汎用的な解法がなく難しいところがありますが、強化学習のライブラリであるkeras-rl + gymを組み合わせることで、お手軽にそこそこの精度のものが開発できるのではないかと感じました。各ステップでの実行プロセスやリセット時の操作、ログ出力などスクラッチで書くとなかなか大変ですが、ライブラリの使用でそのコストを大幅に下げることができます。実際、上の程度の量であれば、ライブラリのインストールから動くものを作るまで半日程度の時間があれば十分でした。

一方で以下のような難しさも感じました。

• observationとして与える特徴量やactionとして取りうる選択肢を決めるのが難しい。うまいobservation, actionの組み合わせを与えないと全く学習してくれない
• 変更できるパラメータがネットワークの構造や訓練の各種パラメータなど多岐にわたり、チューニングが難しい

特に一点目については試行錯誤が必要であり、苦労しました。AIだからうまく学習してくれるかなと思って、observationとして次元が大きな特徴量を加工せずにそのまま入れたり、actionの選択肢の数を大きくしてみたりしたのですがほとんど学習が進みませんでした。

実際に、上ではobservationやactionとして取りうる選択はほとんど経験的な方法を採用してしまっており強化学習の良さを殺してしまっていると感じました。また、今回実装したものが深層強化学習を使用しないアルゴリズムよりも良いものであるかどうかは非自明です。

何をどう学習させるか、AIを使うのは簡単ですが、その「気持ち」と「ふるまい」を理解して使いこなすのは難しいものだと感じました。