Rustで最短経路を見つけよう
フォルシア株式会社でエンジニアをしている松本です。業務ではRustでインメモリデータベースを開発しています。
日常生活においても、最短経路を求めたいことはよくあると思います。例えば旅先でホテルまでの行き方を調べているとき、ボルダリングでオブザベをしているとき、知り合いを何人挟めばトランプ大統領につながるか考えているとき、マンムーにフリーズドライを遺伝させたいとき、おそらくあなたは最短経路について考えています。
例示した構造は頂点と辺からなるグラフとして表現することができ、グラフ上のある点からある点への最も短い経路を見つける問題を最短経路問題と言います。この記事では、Rustで最短経路問題を解くアルゴリズムであるダイクストラ法とワーシャルフロイド法を実装します。最短経路長だけを求めるのではなく、経路復元と呼ばれる最短経路の出力も実装します。
単一始点からの最短経路
まずは単一始点からの最短経路を求めましょう。負の距離を持った辺が無い場合、ダイクストラ法(Dijkstra's algorithm)というアルゴリズムが知られています。これは、既に最短経路で到達した頂点群(A)のどれかと隣接している頂点のうち、最も始点からの距離が短い頂点をAに追加していくアルゴリズムです。
なんとRustの公式ドキュメントでstd::collections::binary_heapのサンプルとしてダイクストラ法の実装が例示されています(アルゴリズムの本体部分を抜粋したものが下記)。
// Dijkstra's shortest path algorithm.
// Start at `start` and use `dist` to track the current shortest distance
// to each node. This implementation isn't memory-efficient as it may leave duplicate
// nodes in the queue. It also uses `usize::MAX` as a sentinel value,
// for a simpler implementation.
fn shortest_path(adj_list: &Vec<Vec<Edge>>, start: usize, goal: usize) -> Option<usize> {
// dist[node] = current shortest distance from `start` to `node`
let mut dist: Vec<_> = (0..adj_list.len()).map(|_| usize::MAX).collect();
let mut heap = BinaryHeap::new();
// We're at `start`, with a zero cost
dist[start] = 0;
heap.push(State { cost: 0, position: start });
// Examine the frontier with lower cost nodes first (min-heap)
while let Some(State { cost, position }) = heap.pop() {
// Alternatively we could have continued to find all shortest paths
if position == goal { return Some(cost); }
// Important as we may have already found a better way
if cost > dist[position] { continue; }
// For each node we can reach, see if we can find a way with
// a lower cost going through this node
for edge in &adj_list[position] {
let next = State { cost: cost + edge.cost, position: edge.node };
// If so, add it to the frontier and continue
if next.cost < dist[next.position] {
heap.push(next);
// Relaxation, we have now found a better way
dist[next.position] = next.cost;
}
}
}
// Goal not reachable
None
}
データの持ち方
グラフを表現する方法として、各頂点について隣接する(ある辺の両端になっている)頂点リスト(あるいは辺の情報)を保持する隣接リスト(adjacency list)と、各頂点対について共有する辺があればその辺の情報を記録する隣接行列(adjacency matrix)があります。ダイクストラ法は隣接している頂点を効率よく見つけたいため、隣接している頂点リストを保持する隣接リストを使うほうが効率が良いです。
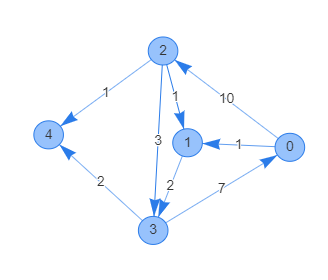
例としてこのような有向グラフを隣接リストで表現すると下記のように表すことができます。
let graph = vec![
vec![Edge { node: 2, cost: 10 }, Edge { node: 1, cost: 1 }],
vec![Edge { node: 3, cost: 2 }],
vec![
Edge { node: 1, cost: 1 },
Edge { node: 3, cost: 3 },
Edge { node: 4, cost: 1 },
],
vec![Edge { node: 0, cost: 7 }, Edge { node: 4, cost: 2 }],
vec![],
];
経路復元
さて、上述の実装では最短経路長だけが返却され、具体的な経路は明らかではありませんでした。具体的な経路を求める方法を考えましょう。
出力したい経路情報path = [start, ..., goal]とstartから各頂点への最短経路長情報distについて考えます。d= dist[path[i]] であるときpath[i-1]はd' = dist[path[i-1]]かつ頂点i-1から頂点iへ距離d-d'の辺を持っているはずです。このような頂点を探すことで最短経路を最短経路長の情報から復元することができます。この方法を素直に実装するとVを頂点数、Lを経路長として最悪計算量O(V^2・L)になってしまいます。
最短経路を求める際に1つ前の頂点情報を記録することでO(L)で復元することができます。下記の実装ではpre_nodeに記録しながら最短経路長を更新しています。
use std::cmp::Ordering;
use std::collections::BinaryHeap;
use std::usize;
// BinaryHeapに渡すStateの実装
#[derive(Copy, Clone, Eq, PartialEq)]
struct State {
cost: usize,
position: usize,
pre_node: usize,
}
impl Ord for State {
fn cmp(&self, other: &State) -> Ordering {
other
.cost
.cmp(&self.cost)
.then_with(|| self.position.cmp(&other.position))
}
}
impl PartialOrd for State {
fn partial_cmp(&self, other: &State) -> Option<Ordering> {
Some(self.cmp(other))
}
}
struct Edge {
node: usize,
cost: usize,
}
fn shortest_path(
adj_list: &Vec<Vec<Edge>>,
start: usize,
goal: usize,
) -> Option<(usize, Vec<usize>)> {
let mut dist: Vec<_> = (0..adj_list.len()).map(|_| usize::MAX).collect();
let mut pre_nodes: Vec<_> = (0..adj_list.len()).map(|i| i).collect();
let mut heap = BinaryHeap::new();
dist[start] = 0;
heap.push(State {
cost: 0,
position: start,
pre_node: 0,
});
while let Some(State {
cost,
position,
pre_node,
}) = heap.pop()
{
if cost > dist[position] {
continue;
}
pre_nodes[position] = pre_node;
if position == goal {
let mut v = goal;
let mut path = vec![goal];
while v != start {
path.push(pre_nodes[v]);
v = pre_nodes[v];
}
path.reverse();
return Some((cost, path));
}
for edge in &adj_list[position] {
let next = State {
cost: cost + edge.cost,
position: edge.node,
pre_node: position,
};
if next.cost < dist[next.position] {
heap.push(next);
dist[next.position] = next.cost;
}
}
}
// Goal not reachable
None
}
具体的なグラフと始点・終点を与え、結果が正しいことを確認しましょう。
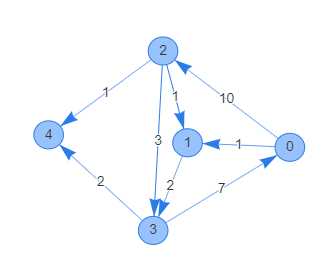
fn main() {
let graph = vec![
vec![Edge { node: 2, cost: 10 }, Edge { node: 1, cost: 1 }],
vec![Edge { node: 3, cost: 2 }],
vec![
Edge { node: 1, cost: 1 },
Edge { node: 3, cost: 3 },
Edge { node: 4, cost: 1 },
],
vec![Edge { node: 0, cost: 7 }, Edge { node: 4, cost: 2 }],
vec![],
];
// fn shortest_path(
// adj_list: &Vec<Vec<Edge>>,
// start: usize,
// goal: usize,
// ) -> Option<(usize, Vec<usize>)>
assert_eq!(shortest_path(&graph, 0, 1), Some((1, vec![0, 1])));
assert_eq!(shortest_path(&graph, 0, 3), Some((3, vec![0, 1, 3])));
assert_eq!(shortest_path(&graph, 3, 0), Some((7, vec![3, 0])));
assert_eq!(shortest_path(&graph, 0, 4), Some((5, vec![0, 1, 3, 4])));
assert_eq!(shortest_path(&graph, 4, 0), None);
}
全点対間の最短経路
続いて、全点対間の最短経路を求めるワーシャルフロイド法(Warshall-Floyd Algorithm)についても実装していきましょう。
データの持ち方
各頂点対について辺を持っているかを高速に調べたいため、隣接行列を使用します。隣接リストで表現したのと同じグラフは隣接行列では下記のように表せます。
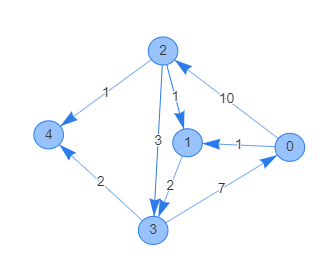
let mut adj_matrix = vec![
vec![None, Some(1), Some(10), None, None],
vec![None, None, None, Some(2), None],
vec![None, Some(1), None, Some(3), Some(1)],
vec![Some(7), None, None, None, Some(2)],
vec![None, None, None, None, None],
];
※Noneは辺がないこと、Some(x)は距離xの辺があることと対応しています。
経路復元
ダイクストラ法と同様に1つ前の情報を保持しておいて、終点から始点へ後ろ向きに遡っても良いのですが、next[i][j] =「頂点iから頂点jに行くとき、頂点iの次に通る頂点」というように更新していくことで、直感的に前からたどることができるようになります。
実装を示します。上述の adj_matrix を dist として下記の warshall_floyd 関数に渡します。
fn warshall_floyd(dist: &mut Vec<Vec<Option<usize>>>) -> Vec<Vec<usize>> {
let n = dist.len();
let mut next = vec![];
// next[i][j] = j で初期化
for i in 0..n {
next.push((0..n).map(|j| j).collect::<Vec<usize>>());
}
for k in 0..n {
for i in 0..n {
for j in 0..n {
if let (Some(dik), Some(dkj)) = (dist[i][k], dist[k][j]) {
if dist[i][j].is_none() || dist[i][j].unwrap() > dik + dkj {
dist[i][j] = Some(dik + dkj);
next[i][j] = next[i][k];
}
}
}
}
}
next
}
隣接行列を最短経路の行列と見て破壊的に更新しながら、次の頂点を記録します。
更新された最短経路の行列と次の頂点を記録した行列を始点から終点にたどることで経路復元が可能です。
fn shortest_path(
dist: &Vec<Vec<Option<usize>>>,
next: &Vec<Vec<usize>>,
start: usize,
goal: usize,
) -> Option<(usize, Vec<usize>)> {
if dist[start][goal].is_none() {
return None;
}
let mut path = vec![start];
let mut node = start;
while node != goal {
path.push(next[node][goal]);
node = next[node][goal];
}
Some((dist[start][goal].unwrap(), path))
}
こちらも同様に動作が確認できます。
fn main() {
let mut dist = vec![
vec![None, Some(1), Some(10), None, None],
vec![None, None, None, Some(2), None],
vec![None, Some(1), None, Some(3), Some(1)],
vec![Some(7), None, None, None, Some(2)],
vec![None, None, None, None, None],
];
let next = warshall_floyd(&mut dist);
assert_eq!(shortest_path(&dist, &next, 0, 1), Some((1, vec![0, 1])));
assert_eq!(shortest_path(&dist, &next, 0, 3), Some((3, vec![0, 1, 3])));
assert_eq!(shortest_path(&dist, &next, 3, 0), Some((7, vec![3, 0])));
assert_eq!(shortest_path(&dist, &next, 0, 4), Some((5, vec![0, 1, 3, 4])));
assert_eq!(shortest_path(&dist, &next, 4, 0), None);
}
まとめ
最短経路問題について具体的な経路を求める方法の解説とRustでの実装例を示しました。
私はまだ実務で最短経路問題を解いたことはありませんが、グラフ理論の別の問題である最小費用流のアルゴリズムが使える場面があり、色々なアルゴリズムを知っておくことは大切だと考えています。
GoogleカレンダーとSlackからの情報で「グループ分け」シャッフルランチはじめました~テクノロジー編~
皆さんも好きな言語でいろいろなアルゴリズムを実装してみてください。
また、フォルシアには競技プログラミング部があり、先日行われたPG BATTLE 2019では企業の部248チーム中9位の成績を収めました。フォルシアで働くことに興味がある方はAtCoderJobsからぜひご連絡ください!
松本 健太郎
フォルシア4年目のエンジニア。
Rustでインメモリデータベースの開発を行っている。



