経済学の問題をJavaScriptで解いてみる

2019.12.06

アドベントカレンダー2019 エンジニアテクノロジー

JavaScript 2 Advent Calendar 2019 6日目の記事です。

こんにちは。2019年新卒入社エンジニアの中曽です。
私は経済学部卒で、入社してから本格的にプログラミングに触れ始めました。

現在の業務ではJavaScriptというプログラミング言語を主に使用しており、この記事では、経済学部卒という背景と合わせて経済学の問題をJavaScriptで解いてみます。

フォルシアには経済学部卒のエンジニアも少なからず在籍し活躍しており、この記事を読んで経済学部の方もプログラミングをやってみたいと思う機会になれば幸いです。もちろん経済学部ではない方でも、経済学に興味を持ってもらうきっかけになると嬉しいです。

ゲーム理論

初めに、何の問題を解くかを決定する必要がありますね。

例えば、ミクロ経済学には消費者理論・生産者理論であったり、マクロ経済学には貨幣市場・労働市場であったりテーマにできそうなものは色々あります。
その数ある問題の中で、日常生活でも関わってくる場面があり興味を持ってもらいやすいと思うので、ゲーム理論を取り上げたいと思います。

簡単に説明すると、ゲーム理論とは、複数の利害関係を持つプレイヤーがいる状況で、それぞれの利得を考えて合理的に意思決定を行う理論のことです。
先程日常生活でも関わってくる場面があると述べましたが、例えば野球での打者と投手の駆け引きもゲーム理論のフレームワークを使って表現することができます。

囚人のジレンマ

次に、ゲーム理論の思考方法に関して有名な例題を出して説明します。

ある犯罪によって2人の容疑者が逮捕され、それぞれが 意思疎通のできない別々の部屋で尋問を受けている。
この時、2人がとる行動は「自白する」or「自白しない」の2択で、それぞれの行動の結果、下記の判決がくだされることが予め分かっているものとします。

片方が「自白する」、もう一方は「自白しない」を選択した場合
- 「自白する」を選択した方は無罪(懲役0年)
- 「自白しない」を選択した方は懲役10年
両方が「自白しない」を選択した場合は、両方が懲役1年
両方が「自白する」を選択した場合は、両方が懲役5年

これを標準型ゲームとして表現し、図示すると、下の表のようになります。

「自白する」をA、「自白しない」をBとし、1文字目にプレイヤー1の選択が来るようにしています。例えばAB(0, -10)は、プレイヤー1が「（A）自白する」、プレイヤー2が「（B）自白しない」場合となります。

プレイヤー1 ＼ 2	（A）自白する	（B）自白しない
（A）自白する	AA (-5, -5)	AB (0, -10)
（B）自白しない	BA (-10, 0)	BB (-1, -1)

上の図を説明すると...

プレイヤー2が「（A）自白する」と考えると、プレイヤー1の利得は

「（A）自白する」を選択した場合→ -5
「（B）自白しない」を選択した場合→ -10
→「（A）自白する」を選択した方が利得が大きくなる

プレイヤー2が「（B）自白しない」と考えると、プレイヤー1の利得は

「（A）自白する」を選択した場合→ 0
「（B）自白しない」を選択した場合→ -1
→「（A）自白する」を選択した方が利得が大きくなる

プレイヤー1はプレイヤー2の選択によらず、常に「（A）自白する」を選択したほうが利得が大きくなります。プレイヤー2の目線で考えた場合も同じような結果になります。
それぞれのプレイヤーは個人の利益を優先して考えた場合、相手がどちらの選択をする場合で考えても「（A）自白する」を選択した方が得になります。

選択したものに〇を付けてみます。

プレイヤー1 ＼ 2	（A）自白する	（B）自白しない
（A）自白する	AA (〇 -5, 〇 -5)	AB (〇 0, -10)
（B）自白しない	BA (-10, 〇 0)	BB (-1, -1)

その結果、AA(-5, -5)がお互いに合理的な判断をした結果となります。これは ナッシュ均衡になっています。どちらにも〇が付いていますね。

ナッシュ均衡をもう少し説明すると、ナッシュ均衡とは「全てのプレイヤーが本人以外の行動を所与として、全てのプレイヤーが互いに最適な戦略を取っている状態」となります。ナッシュ均衡から自分だけが戦略を変更しても利得を上げることができない状態となります。
ちなみに、全体としてはBB(-1, -1)が最適なのにも関わらず、お互いに合理的な判断をした結果AA(-5, -5)がナッシュ均衡となります。これが囚人のジレンマと呼ばれる所以です。

実際に解いてみる

下記の利得表で表現される標準型ゲームのナッシュ均衡を求めるプログラムを作成したいと思います。

プレイヤー1 ＼ 2	A	B
A	AA (a, b)	AB (c, d)
B	BA (e, f)	BB (g, h)

プログラムとして表現する際に、利得表を下記のデータ構造で表現し、関数を作成するにあたり、下のような入力と出力を設定します。

入力

const result = {
	"AA": {player1: a, player2: b},
	"AB": {player1: c, player2: d},
	"BA": {player1: e, player2:  f},
	"BB": {player1: g, player2: h}
}

　1つ目の戦略をA、2つ目の戦略をBとしており、player1の戦略を1文字目に表しています。
　"AA"等の下位のオブジェクトは、player1,2のそれぞれの利得を示しています。

出力

ナッシュ均衡を、AA, AB, BA,BB が含まれる配列の形で返す。
　ex) ["AA"]

実装

それでは、コードを書いていきます。

// ナッシュ均衡を求める関数
const calcNash = (obj) => {
    // 相手のそれぞれの選択に対する最適な選択を決める
    const p1Strategy1 = getMaxOption(obj, "player1", ["AA", "BA"]);
    const p1Strategy2 = getMaxOption(obj, "player1", ["AB", "BB"]);
    const p2Strategy1 = getMaxOption(obj, "player2", ["AA", "AB"]);
    const p2Strategy2 = getMaxOption(obj, "player2", ["BA", "BB"]);
    // 2人のプレイヤーが同じ選択をする場合、ナッシュ均衡となる 
    const nash = [p1Strategy1, p1Strategy2].filter(elm => {
        return elm === p2Strategy1 || elm === p2Strategy2;
    });
    return nash;
};

// 利得が最大になる選択を決定する関数
const getMaxOption = (obj, player, array) => {
    // 適当に初期値を設定(利得の最小値より小さくする必要がある)
    let maxProfit = -100;
    let maxOption = "";
    array.forEach(elm => {
        Object.keys(obj).forEach(key => {
            if (key === elm && obj[key][player] > maxProfit) {
                maxProfit = obj[key][player];
                maxOption = key;
            }
        }); 
    });
    return maxOption;
};

const result = {
	"AA": {player1:  -5, player2:  -5},
	"AB": {player1:   0, player2: -10},
	"BA": {player1: -10, player2:   0},
	"BB": {player1:  -1, player2:  -1}
};

console.log(calcNash(result)); // ['AA']

コードの説明

書いたコードについて説明します。

ナッシュ均衡を求める関数(calcNash)とは別に、利得が最大になる選択を決定する関数(getMaxOption)を分けて作成しました。
getMaxOption関数で相手のそれぞれの選択に対する最適反応を求めた後、calcNash関数でナッシュ均衡を求めるという流れになっています。

getMaxOption関数での処理

array.forEach...引数で指定された配列に対して繰り返し処理を行います。
ex) ["AA", "BB"]
Object.keys(obj).forEach...引数で指定されたオブジェクトに対して繰り返し処理を行います。
if文での処理...配列の要素とオブジェクトのkeyが合致している、かつ指定されたプレイヤーの利得が、以前選択した利得より大きくなる場合に、maxProfitとmaxOptionを更新します。

calcNash関数での処理

p1Starategy1等などの定数...getMaxOption関数を呼び、相手のそれぞれの選択に対する最適な選択を決めます。
nash定数...filter関数を使用してプレイヤー1に対して繰り返し処理をすることで、両プレイヤーが同じ選択をした場合にのみ返り値を渡す配列に結果を抜き出します。

囚人のジレンマのケースで考えると、
プレイヤー1が選択をする際、p1Strategy1で"AA"、p1Strategy2で"AB"が選ばれます。
プレイヤー2が選択をする際、p2Strategy1で"AA"、p2Strategy1で"BA"が選ばれます。
よって、両方が"AA"の選択を行うため、"AA"がナッシュ均衡として返されるという処理になっています。

確率を含めたゲーム理論

しかし、上記では対応できないケースもあります。

例えば、次のようなケースです。

流行の先端を行くリーダーと、リーダーの真似をしようとするフォロワーという2人のプレイヤーがいる。
リーダーにとってはフォロワーと異なる服を着ると利得が高いが、フォロワーにとってはリーダーと同じ色を着ると利得が高い。

リーダー＼フォロワー	（A）赤色の服 q	（B）青色の服 1 - q
（A）赤色の服 p	AA (-1, 〇 1)	AB (〇 1, -1)
（B）青色の服 1 - p	BA (〇1, -1)	BB (-1, 〇-1)

ナッシュ均衡を求めようとしても、お互いの選択が一致するものが無いため求めることができません。

この場合、複数の戦略を確率的に混ぜる「混合戦略」というものを行うということになり、期待される利得を最大化するようにそれぞれの選択確率（どちらの服を選ぶかどうかを決める確率）を求め、その確率が均衡点となります。
これに対して、先のコードで求められるのは、「純粋戦略」のナッシュ均衡といわれ、「純粋戦略」とは与えられた状況に対して、毎回同じ行為のみを行う種類の戦略のことを指します。

例えば、上記の例の場合でリーダーが赤色の服を選ぶ確率をp、フォロワーが赤色の服を選ぶ確率をqとすると、リーダーの期待される利得はフォロワーの選択確率によって変わるので、
赤色の服を選んだ場合: u(赤色の服) = AA(-1) × q + AB(1) × (1-q) = -2q + 1
青色の服を選んだ場合: u(青色の服) = BA(1) × q + BB(-1) × (1-q) = 2q - 1
となります。(u(x)はxを選んだときに期待される利得とします。)

u(赤色の服) > u(青色の服)となるのは、-2q + 1 > 2q - 1 すなわちq < 1/2のとき
u(赤色の服) < u(青色の服)となるのは、-2q + 1 < 2q - 1 すなわちq > 1/2のとき
u(赤色の服) = u(青色の服)となるのは、-2q + 1 = 2q - 1 すなわちq = 1/2のときです。

これをまとめると、

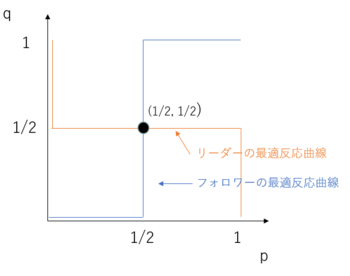
q < 1/2のとき、p = 1 (「(A)赤色の服」を選ぶ)
q = 1/2のとき、0 <= p <= 1
q > 1/2のとき、p = 0 (「(B)青色の服」を選ぶ)

となります。

同様にすると、フォロワーについては、

p < 1/2のとき、q = 0(「(B)青色の服」を選ぶ)
p = 1/2のとき、0 <= q <= 1
p > 1/2のとき、q = 1(「(A)赤色の服」を選ぶ)

となります。

これを基に、それぞれのプレイヤーが相手の選択確率に対する反応を図示した曲線（最適反応曲線と呼ばれる）のグラフの交点が、混合戦略におけるナッシュ均衡となります。

それでは、コードを書いていきます。

引数は純粋戦略と同様な形にし、出力は次のように設定します。

出力

配列の中に、ナッシュ均衡となる確率のペアを配列として入れて返す。
　ex) [[0.5, 0.5]]

// ナッシュ均衡を求める関数
const calcNash = (obj) => {
    // 相手のそれぞれの選択に対する最適な選択を決める
    const p1Strategy1 = getMaxOption(obj, "player1", ["AA", "BA"]);
    const p1Strategy2 = getMaxOption(obj, "player1", ["AB", "BB"]);
    const p2Strategy1 = getMaxOption(obj, "player2", ["AA", "AB"]);
    const p2Strategy2 = getMaxOption(obj, "player2", ["BA", "BB"]);
    
    let nash = [];
    const p1Prob = calcProbability(obj, "player2");
    const p2Prob = calcProbability(obj, "player1"); 
    nash.push([p1Prob, p2Prob]);
    if (p1Strategy1 === p2Strategy1 ) {
        nash.push([1,1])
    }
    if (p1Strategy2 === p2Strategy2) {
        nash.push([0,0])
    }
    return nash;
};
const getMaxOption = (obj, player, array) => {
    // 適当に初期値を設定(利得の最小値より小さくする必要がある)
    let maxProfit = -100;
    let maxOption = "";
    array.forEach(elm => {
        Object.keys(obj).forEach(key => {
            if (key === elm && obj[key][player] > maxProfit) {
                maxProfit = obj[key][player];
                maxOption = key;
            }
        }); 
    });
    return maxOption;
};
// 戦略を選択する確率を算出する関数
const calcProbability = (obj, player) => {
    const prob = player === "player1" ? (obj["BB"][player] - obj["AB"][player]) / (obj["AA"][player] - obj["AB"][player] - obj["BA"][player] + obj["BB"][player])
                                      : (obj["BB"][player] - obj["BA"][player]) / (obj["AA"][player] - obj["BA"][player] - obj["AB"][player] + obj["BB"][player]);
    
    return prob;
};
const result = {
    "AA": {player1: -1, player2:  1},
    "AB": {player1:  1, player2: -1},
    "BA": {player1:  1, player2: -1},
    "BB": {player1: -1, player2:  1}
};
console.log(calcNash(result)); // [[0.5, 0.5]]

処理として加えたのは、calcNash関数において、calcProbability関数を呼び出し確率を求めるという部分です。

calcProbability関数での処理

ここの確率は、各プレイヤーがAを選んだ時とBを選んだ時のそれぞれの期待利得が合致する確率を求めます。例えばプレイヤー1の期待利得は、プレイヤー2の確率によって左右されるので、p2Probの引数に、"player1"が入ってこの関数は呼び出されます。
また、確率を求める式は、例えば-2q + 1 = 2q - 1といった式を予め移項して処理するようにしています。

calcNash関数での処理

ナッシュ均衡時の確率p1Prob1,p2Prob（p1Prob: プレイヤー1がAを選択する確率、p2Prob: プレイヤー2がAを選択する確率）の組み合わせを返します。

if文を追加したのは、混合戦略において上で求めた確率（グラフ上の交点になる）の他に、下の図のように(0, 0), (1, 1)で交点を持つ場合があるからです。確率を用いる混合戦略の中でも、各プレイヤーがそれぞれ相手がAという行動をするならば自分もAを行い、相手がBという行動をするならば自分もBを行った方が利得が高い場合です。
これは純粋戦略における場合と同じ要領で求めることができるので、先に使用したgetMaxOption関数を再度利用しています。下の問題がその例です。

男女の争い

男(プレイヤー1)＼女(プレイヤー2)	（A）野球を見る q	（B）買い物に行く 1 - q
（A）野球を見る p	AA (4, 1)	AB (0, 0)
（B）買い物に行く 1-p	BA (0, 0)	BB (1, 4)

相手がどちらを選択するかは絶対的には決定されないが、もし相手がを野球を見るなら一緒に野球を見た方が利得が大きく、買い物に行くなら買い物に行った方がお互い利得が大きいといった内容ですね。

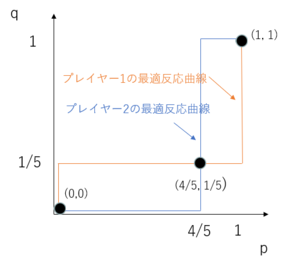
関数の実行結果は下記のようになります。

console.log(calcNash(result)); // [ [ 0.8, 0.2 ], [ 1, 1 ], [ 0, 0 ] ]

まとめ

この記事では経済学の分野からゲーム理論を取り上げ、JavaScriptを使って、標準型ゲームの混合戦略も含めたナッシュ均衡を求めました。
この記事でゲーム理論について興味が出てきたという方がいれば、もっと調べてもらえると嬉しいです。

一方、ゲーム理論は分かるけどもプログラミングに関してはあまり経験がないという方も、この機会に触れてみるのも面白いと思います。

フォルシアでは、需要量を予測し、供給量に応じて最適な販売価格を提示するダイナミックプライシングを扱っています。計量経済学的な面白さもある分野なので、興味のある方はぜひ話を聞きに来てみてください。

この記事を書いた人

中曽勇成

2019年新卒入社。検索プラットフォーム事業部所属のエンジニア。
先日、社内の資格支援制度を使って基本情報技術者試験の資格を取得した。

経済学の問題をJavaScriptで解いてみる

ゲーム理論

囚人のジレンマ

実際に解いてみる

入力

出力

実装

コードの説明

getMaxOption関数での処理

calcNash関数での処理

確率を含めたゲーム理論

出力

calcProbability関数での処理

calcNash関数での処理

男女の争い

まとめ

中曽勇成

関連記事

wasm-bindgenを触ってみよう！RustとWebAssemblyが同時に学べる

サマーインターン1期生より愛を込めて

AtCoder灰・茶・緑色の方必見！二分探索を絶対にバグらせないで書く方法

社会人1年目の自分に送るアドバイス集

経済学の問題をJavaScriptで解いてみる

ゲーム理論

囚人のジレンマ

実際に解いてみる

入力

出力

実装

コードの説明

getMaxOption関数での処理

calcNash関数での処理

確率を含めたゲーム理論

出力

calcProbability関数での処理

calcNash関数での処理

男女の争い

まとめ

中曽 勇成

関連記事

wasm-bindgenを触ってみよう！RustとWebAssemblyが同時に学べる

サマーインターン1期生より愛を込めて

AtCoder灰・茶・緑色の方必見！二分探索を絶対にバグらせないで書く方法

社会人1年目の自分に送るアドバイス集

中曽勇成