プログラミング言語ではなく、フォルシアの高速検索の鍵を握るSQLで数独を解く
技術本部の小海です。フォルシアでは旅行サイトの提案・開発・運用を行っています。今回はSQLというデータベース言語を利用し、数独を解く方法をご紹介します。
※この記事は、SQLを書いたことがある人、これからSQLを勉強したい人を対象としています。
動作環境
- PostgreSQL 9.6.8
- 別のDBを使用する場合、適応SQLを書き換える必要があります。
- CentOS 7.5(仮想環境 1CPU メモリ8GB)
- PostgreSQLが動作する環境であればスペックはあまり問題ありません。
解き方の方針
まず、数独の問題をSQLで扱いやすくするため文字列で扱うこととします。
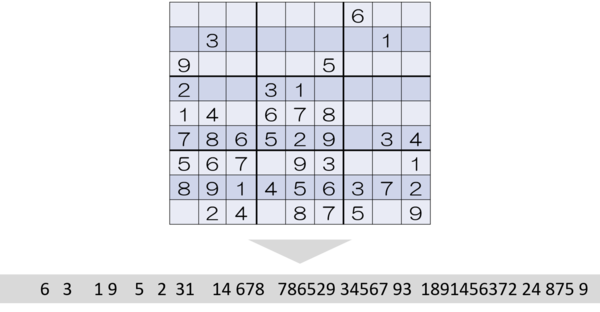
※空欄は半角スペースとしています。
その後、数独のルールに従って、数字を一つずつ埋めていきます。
再帰with句
プログラミング言語ではfor文などの繰り返しがありますが、SQLで行う場合、再帰with句を利用します。
再帰with句とは目的の結果になるまで行を追加していく場合などによく使われる構文です。
WITH RECURSIVE rec AS ( -- 初期値 SELECT 5 AS num -- 再帰with句で追加されていく行 UNION ALL SELECT num - 1 FROM rec -- 終了条件 WHERE num > 1 ) SELECT * FROM rec;
num ----- 5 4 3 2 1 (5 rows)
下記のような再帰with句が書ければ、SQLでも数独を解くことができます。
WITH RECURSIVE _sudoku AS (
-- 初期値
SELECT ' 6 3 1 9 5 2 31 14 678 786529 34567 93 1891456372 24 875 9' AS kekka
-- 再帰with句で追加されていく行
UNION ALL
SELECT '{数独のルールに従って1つ埋めた文字列}'
FROM _sudoku
-- 終了条件
WHERE '{挿入できる数字がなくなった}'
)
SELECT * FROM _sudoku;
想定される結果
kekka
-----------------------------------------------------------------------------------
6 3 1 9 5 2 31 14 678 786529 34567 93 1891456372 24 875 9
4 6 3 1 9 5 2 31 14 678 786529 34567 93 1891456372 24 875 9
4 3 6 3 1 9 5 2 31 14 678 786529 34567 93 1891456372 24 875 9
~ 中略 ~
472931658635842917918765423259314786143678295786529134567293841891456372324 875 9
4729316586358429179187654232593147861436782957865291345672938418914563723241875 9
472931658635842917918765423259314786143678295786529134567293841891456372324187569
この方法を使って数独を解いていきましょう!
したごしらえ
途中の計算で使用するテーブルを作成
- 1-9までの数値を持つテーブル (allnum)
DROP TABLE IF EXISTS allnum; CREATE TABLE allnum AS SELECT generate_series(1, 9) AS num ;
postgres=# SELECT * FROM allnum; num ----- 1 2 ~ 中略 ~ 8 9 (9 rows)
- 9×9とグループの情報を持つテーブル (grid)
DROP TABLE IF EXISTS grid; CREATE TABLE grid AS SELECT (i - 1) * 9 + j AS indexof ,i ,j ,(i - 1) / 3 * 3 + 1 + (j - 1) / 3 AS grp FROM allnum n1(i) ,allnum n2(j) ;
postgres=# SELECT * FROM grid;
indexof | i | j | grp
---------+---+---+-----
1 | 1 | 1 | 1
2 | 1 | 2 | 1
~ 中略 ~
80 | 9 | 8 | 9
81 | 9 | 9 | 9
(81 rows)
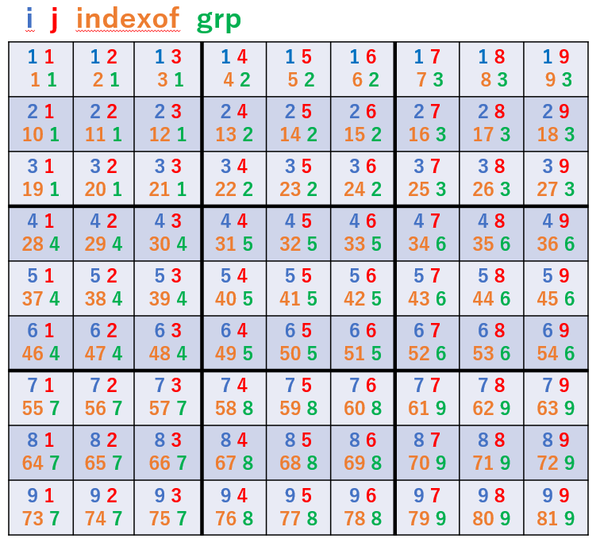
i, j, grp は縦・横・グループで同じ数を使用しないための判定に使用します。 indexof は文字列化された数独の問題を解くために使用します。
数独を解く
実際に解いてみると下記のようになります。
CREATE OR REPLACE FUNCTION sudoku(text) RETURNS text LANGUAGE sql IMMUTABLE AS $$ WITH RECURSIVE _sudoku AS ( -- 初期値 SELECT $1 kekka -- 再帰with句で追加されていく行 UNION ALL( WITH latest AS ( SELECT kekka ,(ROW_NUMBER() OVER())::int parallelid FROM _sudoku ) ,gridnum AS ( SELECT latest.parallelid ,indexof, i, j, grp ,substr(latest.kekka, indexof, 1) AS num FROM latest, grid ) ,used AS ( SELECT gridnums.parallelid ,gridnums.indexof ,array_agg(DISTINCT usednums.num :: int) usednumarray FROM gridnum usednums ,gridnum gridnums WHERE usednums.num <> ' ' AND gridnums.num = ' ' AND usednums.parallelid = gridnums.parallelid AND( usednums.i = gridnums.i OR usednums.j = gridnums.j OR usednums.grp = gridnums.grp ) GROUP BY gridnums.parallelid ,gridnums.indexof ) ,insertnum AS ( SELECT parallelid ,indexof ,usednumarray ,DENSE_RANK() OVER( PARTITION BY used.parallelid ORDER BY ARRAY_LENGTH(used.usednumarray, 1) DESC, indexof ) AS insertorder FROM used ) SELECT overlay(latest.kekka placing allnum.num::text FROM insertnum.indexof FOR 1) AS kekka FROM latest ,allnum ,insertnum WHERE latest.parallelid = insertnum.parallelid AND insertnum.insertorder = 1 AND allnum.num <> ALL(insertnum.usednumarray) ) ) SELECT kekka FROM _sudoku WHERE strpos(kekka, ' ') = 0; $$ ;
解説
上記のSQLは大きく分けると3つのことを行っています。
1. 数字の候補が複数存在する場合に並列で処理する
- latest
2. 最も数字の候補が少ないマス目(indexof) と数字の候補を計算
- gridnum
- used
- insertnum
3. 1の計算結果を元に、最も数字の候補が少ないマス目を埋める
- 再帰with句のSELECT文
1. 数字の候補が複数存在する場合に並列で処理する
latest
- 行程3で数字を埋めたマス目に数字の候補が複数あったとき、再帰with句で複数行が一度に追加されることがあります。
- この後の処理で並列して計算を行うため、番号をふります。
latest AS ( SELECT kekka -- 最新の計算結果 ,(ROW_NUMBER() OVER())::int parallelid -- 並列で処理するために番号をふる FROM _sudoku -- 再帰with )
2. 数字の候補が最も少ないマス目(indexof) を計算
gridnum
- 事前に用意したgridテーブルを使用します。
- 最新の計算結果とマス目の縦・横・グループの情報を結合します。
gridnum AS ( SELECT latest.parallelid -- 並列化番号 ,indexof, i, j, grp -- gridテーブルの情報 ,substr(latest.kekka, indexof, 1) AS num -- そこに存在する数字(空欄は空文字) FROM latest, grid )
used
- マス目ごとに縦・横・グループで既に使用されている数を配列に集約します。
used AS ( SELECT gridnums.parallelid -- 並列化番号 ,gridnums.indexof -- マス目 ,array_agg(DISTINCT usednums.num :: int) usednumarray -- 使用済数配列を作成 FROM gridnum usednums -- 上で計算した結果1(使用済数配列の作成に使用) ,gridnum gridnums -- 上で計算した結果2(基準) WHERE usednums.num <> ' ' -- 空欄じゃないマス AND gridnums.num = ' ' -- 空欄のマス AND usednums.parallelid = gridnums.parallelid -- 並列化番号 AND( usednums.i = gridnums.i -- 横が同じ OR usednums.j = gridnums.j -- 縦が同じ OR usednums.grp = gridnums.grp -- グループが同じ ) GROUP BY gridnums.parallelid -- 並列化番号 ,gridnums.indexof -- マス目ごとに集約 )
途中結果
parallelid | indexof | usednumarray
------------+---------+-------------------
1 | 1 | {1,2,3,5,6,7,8,9}
1 | 2 | {2,3,4,6,8,9}
~ 中略 ~
1 | 76 | {2,3,4,5,6,7,8,9}
1 | 80 | {1,2,3,4,5,7,8,9}
insertnum
- usedで計算した usednumarray を元に、最も数字の候補が少ないマスを計算します。
- ここでは順番をふり、後のSELECT句で insertorder = 1 に絞り込みます。
insertnum AS (
SELECT
parallelid -- 並列化番号
,indexof -- マス目
,usednumarray -- 使用済数の配列
-- 使用済数の配列が長い順(数字の候補が少ない順)に番号をふる
,DENSE_RANK() OVER(
PARTITION BY used.parallelid
ORDER BY ARRAY_LENGTH(used.usednumarray, 1) DESC, indexof
) AS insertorder
FROM used
)
3. 1の計算結果を元に、最も数字の候補が少ないマス目を埋める
- 再帰with句でUNIONされる本体部分のSQLです。
- overlay関数を使用し、数字を埋めています。
- 候補の数字が複数ある場合、複数行が作られます。
SELECT
-- {latest.kekka} を、 {insertnum.indexof} 文字目から {1} 文字分 {allnum.num::text} に置き換える
overlay(latest.kekka placing allnum.num::text FROM insertnum.indexof FOR 1) AS kekka
FROM
latest -- 最新の計算結果
,allnum -- 1-9までの数字
,insertnum -- 1で計算した結果
WHERE
latest.parallelid = insertnum.parallelid -- 並列化への対応
AND
insertnum.insertorder = 1 -- 最も数字の候補が少ないマス目の情報のみを使用
AND
allnum.num <> ALL(insertnum.usednumarray) -- 縦・横・グループで使われていない数字のみを使用
実行してみる
せっかくSQLで関数を作成したので、一気に5問解いてみます。
まずは、数独の問題を持つテーブルを作成します。
DROP TABLE IF EXISTS sudoku_q;
CREATE TABLE sudoku_q AS
SELECT 1 id, ' 6 3 1 9 5 2 31 14 678 786529 34567 93 1891456372 24 875 9'::text as question
UNION SELECT 2, ' 7 3 6 9152 23 48 7418 65 7 9325 876 9341 9215 37 5 18296'
UNION SELECT 3, ' 3 1967 4 8 2 34157 2 62315 68 9 13 68 9 258479 6 2 9143857'
UNION SELECT 4, ' 9 8 7 42 6 3 7 1 2 5 836 992 651 475 63491831 8 7452 9521 63'
UNION SELECT 5, ' 5 3 6 824 7 1 2954167 1 86 2954 6 7 9312 39784 563241 7 9 5283'
;
postgres=# SELECT * FROM sudoku_q ORDER BY id; id | question ----+----------------------------------------------------------------------------------- 1 | 6 3 1 9 5 2 31 14 678 786529 34567 93 1891456372 24 875 9 2 | 7 3 6 9152 23 48 7418 65 7 9325 876 9341 9215 37 5 18296 3 | 3 1967 4 8 2 34157 2 62315 68 9 13 68 9 258479 6 2 9143857 4 | 9 8 7 42 6 3 7 1 2 5 836 992 651 475 63491831 8 7452 9521 63 5 | 5 3 6 824 7 1 2954167 1 86 2954 6 7 9312 39784 563241 7 9 5283 (5 rows)
作成した関数を使って数独を解きます。
postgres=# \timing Timing is on. postgres=# SELECT id, sudoku(question) FROM sudoku_q ORDER BY id; id | sudoku ----+----------------------------------------------------------------------------------- 1 | 472931658635842917918765423259314786143678295786529134567293841891456372324187569 2 | 694857123387142659152639784235481967418976532769325841876293415921564378543718296 3 | 458326719672914385913857426341579268896231574725468193137685942584792631269143857 4 | 235976841178342596694158327867419235541283679923765184752634918316897452489521763 5 | 635217849741893526982456731329541678178632954564789312213978465856324197497165283 (5 rows) Time: 204.773 ms
問題の難易度によって実行速度は変わりますが、1問あたり40ミリ秒で解くことができました!
さいごに
Spookの技術を使って高速化してみた
postgres=# SELECT id, spook_sudoku(question) FROM sudoku_q ORDER BY id; id | spook_sudoku ----+----------------------------------------------------------------------------------- 1 | 472931658635842917918765423259314786143678295786529134567293841891456372324187569 2 | 694857123387142659152639784235481967418976532769325841876293415921564378543718296 3 | 458326719672914385913857426341579268896231574725468193137685942584792631269143857 4 | 235976841178342596694158327867419235541283679923765184752634918316897452489521763 5 | 635217849741893526982456731329541678178632954564789312213978465856324197497165283 (5 rows) Time: 1.555 ms
Spookの技術がどのようにDBの情報を使い高速化しているか、については詳細に書くことができないのですが、ここまで高速化することができました。プログラミング言語ではなくSQLで書くことで数百万個の問題も一度に解くことができます!
このような高速化技術によって、【宿 × 部屋 × 食事有無 × 宿泊人数 × 日数】など、豊富な料金データを持つ旅行サイトの在庫や料金の計算を可能にしています。
入社後はもちろんのこと、フォルシアのインターンでは高速化技術についても学ぶことができます。
興味のある方はぜひ!
小海研太
2012年新卒入社 エンジニア
現在では旅行サイトの提案・開発・運用を主に担当。



