昭和のAIスキルでどこまで立ち向かえるのか　対戦型ゲームAIコンテスト奮闘記

2018.12.16

アドベントカレンダー2018

FORCIAアドベントカレンダー2018 16日目の記事です。

技術本部の小野です。おじさんです。若い人が多い会社なので浮いています：）

最近のゲームAIの進歩はめざましいものがありますが、30年前（第二次AIブームの頃）の AI スキルでどこまで立ち向かえるのか興味があり、年甲斐もなく挑戦してみました。

きっかけ

ことのきっかけはというと、下記サイトを見て興味をもったことです。

昔（80年台後半）アートディンク社（まだある）の地球防衛軍というPCゲームがありました。迎撃機のパーツやアルゴリズムをカスタマイズして敵と戦うものです。あの頃は市販のゲームもBASICで書かれていて改造しやすかったので、カスタマイズ操作を自動化して眺めて楽しむゲームに魔改造したなあ...コア戦争(※1)なんてのも流行ってたし...なんてことを思い出すと、懐かしくなります。

※1 ハッカーの遺言状──竹内郁雄の徒然苔第14回：プログラムで一句詠む | サイボウズ式

対戦型ゲームAIコンテストとは

はじめに、対戦型ゲームAIコンテストについて解説します。

フランス、アメリカを中心にいくつもある。私が参加したのはCodinGameの"Tron Battle"
コンテストといっても期間が限定されているわけでなく、誰でもいつでも参加できる。
一定速度で走る車を操作して、相手を先に囲い込んで動けなくした方が勝ちというゲーム。この車を操作するアルゴリズムを競う
2人～4人まで対戦できる。
ゲーム名「トロン」はおじさんなら知っている80年台の下記SF映画から取られている。
- 1982 - Tron - Trailer - YouTube

ゲームシステム

フロントエンド

素晴らしい！

右上：エディタエリア（emacs モードと vim モードがある）
右下：敵(opponent) 選択エリア
左上：ゲーム（闘技場）エリア
左下：ログエリア

ゲームAIのプログラミング

言語はほぼ何でもつかえる。
STDINから記号列で相手の位置が与えられるので、自分の次の移動位置をSTDOUT に出力すればいい。

対戦

ローカルモード
- 相手を選んで1対1～3までで対戦できる。
- rating はつかない。
グローバルモード（公式戦）
- ランダムに選ばれた相手と計２００ゲーム対戦する（自動対戦）。
- rating が付く。

攻略法というかポリシー

最近のゲームAIの進歩はめざましく、上位に行くには勉強する必要があります。しかし、勉強に時間がかかるので、弱くていいからとりあえず動くプログラムをさくっと作りたい、ということで、昔（30年前位）習った下記3つだけでナンチャッテ版(※2)を作ることにしました。

※2 前の会社では「なんちゃって＊＊＊」という台詞がプロトタイプ版の意味でごく普通に使われていた。開発計画の打ち合わせで「では、なんちゃって版を3月迄に作って...」みたいな感じで使われていた。

Bronze 期

最初はBronze から始まる。1体1の対戦（2人モード）のみ（最近はWoodから始まるようです）。
Legal Move をしないと壁や自分の軌跡に衝突死してすぐ死ぬ。
一番手が速い Perl でとりあえず書いてみた。とりあえずLegal Move するようにはなった。
もうちょっと「知的」なアルゴリズムにしたくなった。

Silver 期

局面評価に昔習った「ボロノイ図」が使えるのではないかと考えた。これは実装も楽そうだ。
おそらくゲームAIの教科書には書いてあると思うが「勉強しない」という方針なので見ていない。
実装した。動きがぐっと知的になった。後ろに回り込まれないよう用心しながら相手に接近するようになった。

そう見えるだけで、実際は期待値の高い方向に動いているに過ぎない
Bossに勝った！Silver に行けた。
silver 期から対戦に3人モード（相手が２人）が追加される。1対1用のアルゴリズムを拡張した。

Gold 期

伸び悩む。勉強せずに上位に行くにはどうすればいいか。。。
上位のプレイヤーはどんな言語で実装しているか調べると、C++が多いことが分かった。
実装言語を Perl から C++ に変更した。４手先まで読めるようになった。
Boss に勝った！ Gold に行けた。
4人モード（相手が3人）を追加した。

Legend 。。。にはいまだ達せず

さすがに naive なアルゴリズムでは限界がある。局面評価の高速化を含めアルゴリズム的に工夫する余地はまだまだあるが未着手。
1対1（プレイヤー数2）だとまあまあだが、プレイヤー数が3以上になると弱くなる。別のアイデアが要るようだ。また局地戦に弱い。
ちなみに１対１だと初期位置（ランダム）だけでほぼ勝敗が決まると言っていい。
上位アルゴリズムは機械学習を導入して相手のアルゴリズムの癖とかを調べているらしい。
機械学習導入となると、ビジョンに基づいて全体を書き直す必要がある。そうなると「学習しない」わけにはいかないので、一旦放置。
到達したランキングはゴールドリーグで 273th/418 。日本人としては4位、 Legend を含めると20位。

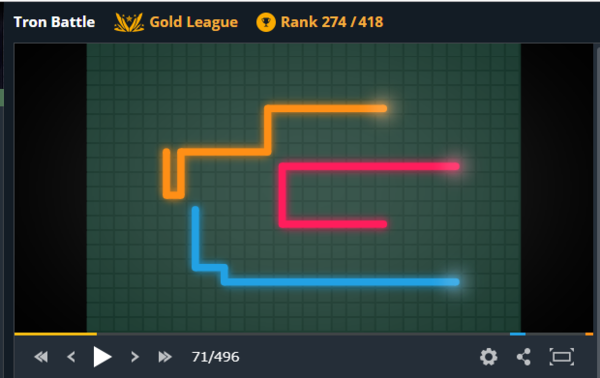
局面評価例

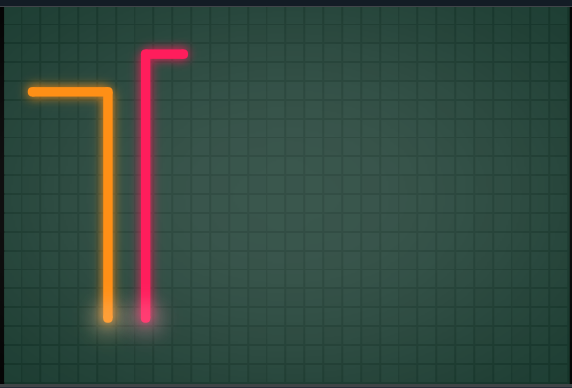
下記は3人プレーで71手目の局面です。私は橙色。ほんのり白く光っている方が現在位置を表しています。

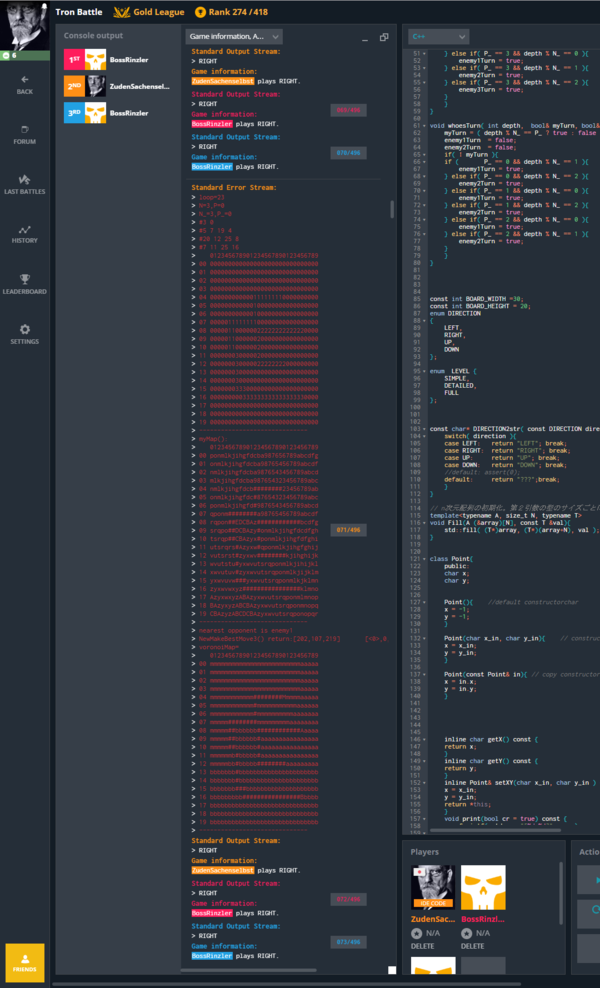
STDERRに局面評価情報等のログを出力しており、後でアルゴリズムを改良するときに使います。

STDERR には下記のような情報が出力されています。

voronoiMap=
   012345678901234567890123456789
00 mmmmmmmmmmmmmmmmmmmmmmmmmaaaaa
01 mmmmmmmmmmmmmmmmmmmmmmmmmaaaaa
02 mmmmmmmmmmmmmmmmmmmmmmmmmaaaaa
03 mmmmmmmmmmmmmmmmmmmmmmmmmaaaaa
04 mmmmmmmmmmmm########Mmmmmaaaaa
05 mmmmmmmmmmmm#mmmmmmmmmmmaaaaaa
06 mmmmmmmmmmmm#mmmmmmmmmmaaaaaaa
07 mmmmm########mmmmmmmmmaaaaaaaa
08 mmmmm##bbbbbb############Aaaaa
09 mmmmm##bbbbbb#aaaaaaaaaaaaaaaa
10 mmmmm##bbbbbb#aaaaaaaaaaaaaaaa
11 mmmmmmb#bbbbb#aaaaaaaaaaaaaaaa
12 mmmmmbb#bbbbb########aaaaaaaaa
13 bbbbbbb#bbbbbbbbbbbbbbbbbbbbbb
14 bbbbbbb#bbbbbbbbbbbbbbbbbbbbbb
15 bbbbbbb###bbbbbbbbbbbbbbbbbbbb
16 bbbbbbbbb################Bbbbb
17 bbbbbbbbbbbbbbbbbbbbbbbbbbbbbb
18 bbbbbbbbbbbbbbbbbbbbbbbbbbbbbb
19 bbbbbbbbbbbbbbbbbbbbbbbbbbbbbb
------------------------------
#: 軌跡
M: 自分の現在位置
A: 敵プレイヤー１の現在位置
B: 敵プレイヤー２の現在位置
m: 自分の領域（なわばり）
a: 敵プレイヤー１の領域
b: 敵プレイヤー２の領域

この局面評価をもとに、自分の領域を増やし相手の領域を減らすような動きを選択します。

アルファベータ、 mini-max 計算例（1対1対戦時）

------------------------------
entered makeBestMove()
	myPoint:[8,18]
	enemyPoint:[17,13]
                makeBestMoveSub(4) returns: [284,245] LEFT < RIGHT > LEFT < RIGHT > 
                makeBestMoveSub(4) returns: [284,245] LEFT < RIGHT > LEFT < UP > 
                makeBestMoveSub(4) returns: [284,245] LEFT < RIGHT > LEFT < DOWN > 
            makeBestMoveSub(3) returns: [284,245] LEFT < RIGHT > LEFT < RIGHT > 
                makeBestMoveSub(4) returns: [284,245] LEFT < RIGHT > UP < RIGHT > 
                makeBestMoveSub(4) returns: [284,245] LEFT < RIGHT > UP < UP > 
                makeBestMoveSub(4) returns: [284,245] LEFT < RIGHT > UP < DOWN > 
            makeBestMoveSub(3) returns: [284,245] LEFT < RIGHT > UP < RIGHT > 
                makeBestMoveSub(4) returns: [284,245] LEFT < RIGHT > DOWN < RIGHT > 
                makeBestMoveSub(4) returns: [284,245] LEFT < RIGHT > DOWN < UP > 
                makeBestMoveSub(4) returns: [284,245] LEFT  DOWN < DOWN > 
            makeBestMoveSub(3) returns: [284,245] LEFT < RIGHT > DOWN < RIGHT > 
        makeBestMoveSub(2) returns: [284,245] LEFT < RIGHT > LEFT < RIGHT > 
                makeBestMoveSub(4) returns: [284,245] LEFT < UP > LEFT < RIGHT > 
                makeBestMoveSub(4) returns: [284,245] LEFT < UP > LEFT < UP > 
            makeBestMoveSub(3) returns: [284,245] LEFT < UP > LEFT < RIGHT > 
                makeBestMoveSub(4) returns: [284,245] LEFT < UP > UP < RIGHT > 
                makeBestMoveSub(4) returns: [284,245] LEFT < UP > UP < UP > 
            makeBestMoveSub(3) returns: [284,245] LEFT < UP > UP < RIGHT > 
                makeBestMoveSub(4) returns: [284,245] LEFT < UP > DOWN < RIGHT > 
                makeBestMoveSub(4) returns: [284,245] LEFT < UP > DOWN < UP > 
            makeBestMoveSub(3) returns: [284,245] LEFT < UP > DOWN < RIGHT > 
        makeBestMoveSub(2) returns: [284,245] LEFT < UP > LEFT < RIGHT > 
    makeBestMoveSub(1) returns: [284,245] LEFT < RIGHT > LEFT < RIGHT > 
                makeBestMoveSub(4) returns: [284,245] UP < RIGHT > LEFT < RIGHT > 
                makeBestMoveSub(4) returns: [284,245] UP < RIGHT > LEFT < UP > 
                makeBestMoveSub(4) returns: [284,245] UP < RIGHT > LEFT < DOWN > 
            makeBestMoveSub(3) returns: [284,245] UP < RIGHT > LEFT < RIGHT > 
                makeBestMoveSub(4) returns: [284,245] UP < RIGHT > RIGHT < RIGHT > 
                makeBestMoveSub(4) returns: [284,245] UP < RIGHT > RIGHT < UP > 
                makeBestMoveSub(4) returns: [284,245] UP < RIGHT > RIGHT < DOWN > 
            makeBestMoveSub(3) returns: [284,245] UP < RIGHT > RIGHT < RIGHT > 
                makeBestMoveSub(4) returns: [284,245] UP < RIGHT > UP < RIGHT > 
                makeBestMoveSub(4) returns: [284,245] UP < RIGHT > UP < UP > 
                makeBestMoveSub(4) returns: [284,245] UP < RIGHT > UP < DOWN > 
            makeBestMoveSub(3) returns: [284,245] UP < RIGHT > UP < RIGHT > 
        makeBestMoveSub(2) returns: [284,245] UP < RIGHT > LEFT < RIGHT > 
                makeBestMoveSub(4) returns: [284,245] UP < UP > LEFT < RIGHT > 
                makeBestMoveSub(4) returns: [284,245] UP < UP > LEFT < UP > 
            makeBestMoveSub(3) returns: [284,245] UP < UP > LEFT < RIGHT > 
                makeBestMoveSub(4) returns: [284,245] UP < UP > RIGHT < RIGHT > 
                makeBestMoveSub(4) returns: [284,245] UP < UP > RIGHT < UP > 
            makeBestMoveSub(3) returns: [284,245]...
Standard Output Stream:
LEFT
Game information:
ZudenSachenselbst plays LEFT

上記の例だと、例えば4行目はこの先

自分が次に LEFT
相手が次に RIGHT
自分が次の次に LEFT
相手が次の次にRIGHT

に動いた場合の局面評価が

自分の縄張り：284
相手の縄張り：245

になることを示しています。4手先の他の手も同様に評価して最善手を選んでいます。最善手の選定にはmini-max 法を、検索の高速化（枝刈り）にはアルファベータ法を利用しています。

アルゴリズムと実装

voronoi図の計算には "Flood Fill" アルゴリズムが利用できます。これは初期の ComputerGraphics の閉領域塗りつぶし処理で利用されていたもので、遅いが実装は楽です。

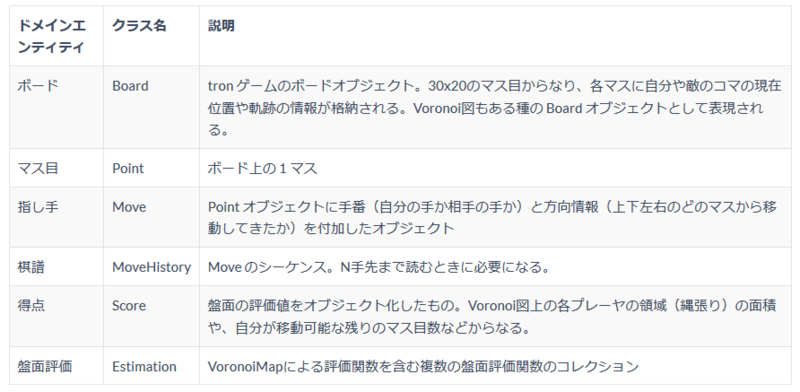
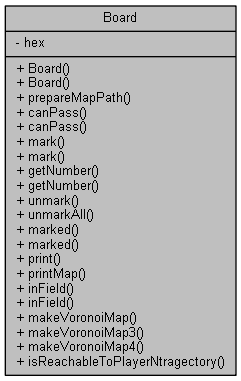
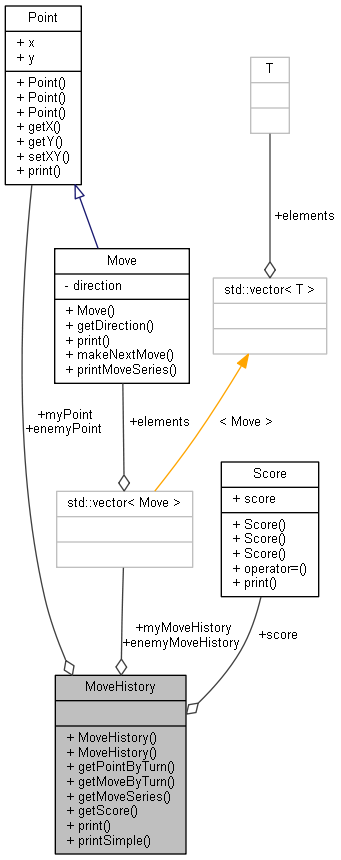
オブジェクト設計

C++ 版に書き直したとき、実装の検証目的で最低限のオブジェクト設計を行いました。

コード例

Voronoi 図の計算周辺について示します。Voronoi 図の計算は2つのステップからなっています。

各プレイヤーがボード上の各マスに何手で到達可能か計算する。この計算をEstimation::mapPath とEstimation::enlargeArea で実装している。
(1) の計算結果を利用して各プレイヤーのVoronoi領域を決定する。各マス目を、もっとも早くそのマス目に到達できるプレイヤーの領域とみなす(Board::makeVoronoiMap)。
上記関数は、N手先まで読んで最善手を決定する関数 Estimation::makeBestMove から呼ばれる。
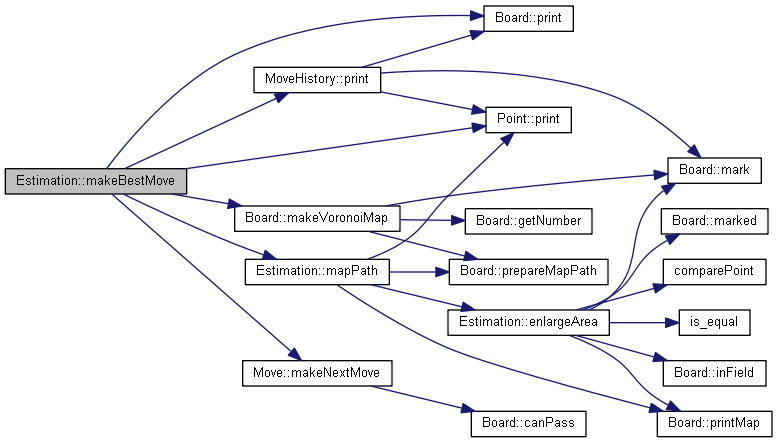
コールグラフを以下に示します。

Board::mapPath

盤面全体のVoronoi 図を計算するのが理想的だが時間がかかります。所要時間を考慮して3つのレベル(SIMPLE, DETAILED, FULL) を設けています。

inline static Board mapPath(const Board& board_arg, const Point& current, LEVEL level = FULL ){

	vector< Point > vec_point;
	vec_point.push_back( current );

    	Board board ( board_arg );
    	board.prepareMapPath();

	int num = 1;

	if( level == SIMPLE ){

	    for( int i = 0; i < 10; i++ ){
		Estimation::enlargeArea( board, vec_point, num );
		if( vec_point.empty()){
		    break;
		}
		num++;
	    }
	} else if( level == DETAILED ){
	    for( int i = 0; i < 40; i++ ){
		Estimation::enlargeArea( board, vec_point, num );
		if( vec_point.empty()){
		    break;
		}
		num++;
	    }
	} else {	// level == FULL
	    while(1){
		Estimation::enlargeArea( board, vec_point, num );
		if( vec_point.empty()){
		    break;
		}
		num++;
	    }
	}

	return board;
}

Estimation::enlargeArea

flood fill アルゴリズムの中心部分です。塗りつぶし中の領域の周縁(fringe) の各マス目に着目して、まだ塗っていない隣接セルをピックアップします。これが次のステップで塗りつぶす対象となります。あわせて塗りつぶし開始位置（各プレイヤーの現在位置）からの距離を計算します。

static void Estimation::enlargeArea( Board& board, vector< Point >& vec_point, short int step ){


	vector< Point > next_point;
	for( int i = 0; i < vec_point.size(); i++){
	    Point point;
	    const Point& cand = vec_point[i];
	    point.x = cand.x;
	    point.y = cand.y;

	    if( Board::inField(point)  && ! board.marked( point ) ){
		board.mark(point, step);
	    }

	    point.x = cand.x+1;
	    point.y = cand.y;
	    if( Board::inField(point)  && ! board.marked( point  ) ){
		next_point.push_back( point );
	    }

	    point.x = cand.x-1;
	    point.y = cand.y;
	    if( Board::inField(point)  && ! board.marked( point  ) ){
		next_point.push_back( point );
	    }

	    point.x = cand.x;
	    point.y = cand.y+1;
	    if( Board::inField(point)  && ! board.marked( point  ) ){
		next_point.push_back( point );
	    }

	    point.x = cand.x;
	    point.y = cand.y-1;
	    if( Board::inField(point)  && ! board.marked( point  ) ){
		next_point.push_back( point );
	    }
	}

	sort( next_point.begin(), next_point.end(), comparePoint );
	vector< Point >::iterator new_end = unique(next_point.begin(),next_point.end(),is_equal);
	next_point.erase(new_end, next_point.end());

	vec_point.clear();
	vec_point = next_point;

	return vec_point;
}

Board::makeVoronoiMap

Board::mapPath で得られた各プレイヤーの到達手数マップを統合してVoronoi 図を生成します。各プレイヤーのVoronoi 領域（なわばり）の面積を返します。

static Board makeVoronoiMap ( const Board& board_arg, const Board& myMap, const Board& enemyMap,
	    	const Point& myPoint, const Point& enemyPoint,
		int& myAreaSize, int& enemyAreaSize ){

	myAreaSize = 0;
	enemyAreaSize = 0;

	Board board(board_arg);
	board.prepareMapPath();

	for(int x = 0; x < BOARD_WIDTH;x++){
	    for(int y = 0; y < BOARD_HEIGHT;y++){
		if( board.getNumber(x,y) < 0 ){
		    continue;
		} 
		if( myMap.hex[x][y]  > 0  && enemyMap.hex[x][y]  > 0 ){	// I and enemy can reach
		    if(         myMap.hex[x][y]  < enemyMap.hex[x][y] ){	// I can reach faster
			board.mark(x,y, '+');
			myAreaSize ++;
		    } else if( myMap.hex[x][y]  == enemyMap.hex[x][y] ){	// same step
			if( P_ == 0 ){	// 
			    board.mark(x,y, '+');
			    myAreaSize ++;
			} else {
			    board.mark(x,y, '-');
			    enemyAreaSize ++;
			}
		    } else {
			board.mark(x,y, '-');
			enemyAreaSize ++;
		    }
		    continue;
		} 
		if( myMap.hex[x][y]  > 0 ){	// I can reach, enemy cannot reach
		    board.mark(x,y, '+');
		    myAreaSize ++;
		    continue;
		} 
		if( enemyMap.hex[x][y]  > 0 ){	// I cannot reach, enemy can erach
		    board.mark(x,y, '-');
		    enemyAreaSize ++;
		    continue;
		} 
	    }
	}
	board.mark( myPoint, 'P');
	board.mark( enemyPoint, 'Q');
	return board;
}

関数の動作説明

上記関数の下記局面での計算例を示します。橙色が私、赤色が敵です。

Flood Fill による自分の mapPath 計算結果は下記となります。
ここで数字は自分の現在位置からの距離（そのマス目に到達するのに何手かかるか）を示します。
a,b,c,... はそれぞれ 10, 11, 12 ... に読み直して下さい。

   012345678901234567890123456789
00 `lmlkjihijklmnopqrstuvwxyzABCDE`
01 `klkjihghijklmnopqrstuvwxyzABCD`
02 `jkjihgf###jklmnopqrstuvwxyzABC`
03 `ijihgfd#ghijklmnopqrstuvwxyzAB`
04 `h#####c#fghijklmnopqrstuvwxyzA`
05 `gfdcb#b#dfghijklmnopqrstuvwxyz`
06 `fdcba#a#cdfghijklmnopqrstuvwxy`
07 `dcba9#9#bcdfghijklmnopqrstuvwx`
08 `cba98#8#abcdfghijklmnopqrstuvw`
09 `ba987#7#9abcdfghijklmnopqrstuv`
10 `a9876#6#89abcdfghijklmnopqrstu`
11 `98765#5#789abcdfghijklmnopqrst`
12 `87654#4#6789abcdfghijklmnopqrs`
13 `76543#3#56789abcdfghijklmnopqr`
14 `65432123456789abcdfghijklmnopq`
15 `7654323456789abcdfghijklmnopqr`
16 `876543456789abcdfghijklmnopqrs`
17 `98765456789abcdfghijklmnopqrst`
18 `a987656789abcdfghijklmnopqrstu`
19 `ba9876789abcdfghijklmnopqrstuv`

敵の mapPath は下記：

   012345678901234567890123456789
00 `nmlkjihijkjklmnopqrstuvwxyzABC`
01 `mlkjihghijijklmnopqrstuvwxyzAB`
02 `lkjihgf###hijklmnopqrstuvwxyzA`
03 `kjihgfd#dfghijklmnopqrstuvwxyz`
04 `j#####c#cdfghijklmnopqrstuvwxy`
05 `ihgfd#b#bcdfghijklmnopqrstuvwx`
06 `hgfdc#a#abcdfghijklmnopqrstuvw`
07 `gfdcb#9#9abcdfghijklmnopqrstuv`
08 `fdcba#8#89abcdfghijklmnopqrstu`
09 `dcba9#7#789abcdfghijklmnopqrst`
10 `cba98#6#6789abcdfghijklmnopqrs`
11 `ba987#5#56789abcdfghijklmnopqr`
12 `a9876#4#456789abcdfghijklmnopq`
13 `98765#3#3456789abcdfghijklmnop`
14 `8765432123456789abcdfghijklmno`
15 `987654323456789abcdfghijklmnop`
16 `a9876543456789abcdfghijklmnopq`
17 `ba98765456789abcdfghijklmnopqr`
18 `cba987656789abcdfghijklmnopqrs`
19 `dcba9876789abcdfghijklmnopqrst`
------------------------------

上記2つから makeVoronoiMap によって作成されたボロノイ図は下記となります。
'+' で示されているのが自分(P)の領域、'-' で示されているのが敵(Q) の領域となります。
敵の領域が明らかに広くてやばい状況であることが判ります：）

   012345678901234567890123456789
00 ++++++++++--------------------
01 ++++++++++--------------------
02 +++++++###--------------------
03 +++++++#----------------------
04 +#####+#----------------------
05 +++++#+#----------------------
06 +++++#+#----------------------
07 +++++#+#----------------------
08 +++++#+#----------------------
09 +++++#+#----------------------
10 +++++#+#----------------------
11 +++++#+#----------------------
12 +++++#+#----------------------
13 +++++#+#----------------------
14 +++++P+Q----------------------
15 +++++++-----------------------
16 +++++++-----------------------
17 +++++++-----------------------
18 +++++++-----------------------
19 +++++++-----------------------

まとめと余談：google のゲームAIに対する布石

30年前のスキル(state of the art)でも、評価関数が良ければそこそこいけることを確認しました。
google は2010 年頃から gameAI コミュニティに投資して、いろいろなサイトやイベントを通じてプレイヤーがアルゴリズムを競うことができるようにしています。彼らの知見は集められて本にもなっています(※3)。アルファ碁のような成果もこのような活動の延長線にあるものであり、短期的な成果ではありません。

※3 Game AI Pro: Collected Wisdom of Game AI Professionals - Google ブックス

この記事を書いた人

小野顕司

技術本部マネージャ
2018年中途入社。
検索精度改善や言語資源の導入等、社内の自然言語処理技術の整備を行っている。

昭和のAIスキルでどこまで立ち向かえるのか　対戦型ゲームAIコンテスト奮闘記

きっかけ

対戦型ゲームAIコンテストとは

ゲームシステム

フロントエンド

ゲームAIのプログラミング

対戦

ランキング

攻略法というかポリシー

Bronze 期

Silver 期

Gold 期

Legend 。。。にはいまだ達せず

局面評価例

アルファベータ、 mini-max 計算例（1対1対戦時）

アルゴリズムと実装

オブジェクト設計

コード例

Board::mapPath

Estimation::enlargeArea

Board::makeVoronoiMap

関数の動作説明

まとめと余談：google のゲームAIに対する布石

小野顕司

関連記事

「CTFを作ってみた」　アドベントカレンダー最終回

学生から社会人、資質の変化は見られるのか　7年ぶりのストレングスファインダーを受けてみた

技術もお笑いも見習い中の新卒2年目エンジニアが語る　フォルシアの顧客チーム

圧縮アルゴリズムZstandardを導入しバッチ処理時間を短縮　データ鮮度を改善した話

昭和のAIスキルでどこまで立ち向かえるのか 対戦型ゲームAIコンテスト奮闘記

きっかけ

対戦型ゲームAIコンテストとは

ゲームシステム

フロントエンド

ゲームAIのプログラミング

対戦

ランキング

攻略法というかポリシー

Bronze 期

Silver 期

Gold 期

Legend 。。。にはいまだ達せず

局面評価例

アルファベータ、 mini-max 計算例（1対1対戦時）

アルゴリズムと実装

オブジェクト設計

コード例

Board::mapPath

Estimation::enlargeArea

Board::makeVoronoiMap

関数の動作説明

まとめと余談：google のゲームAIに対する布石

小野顕司

関連記事

「CTFを作ってみた」 アドベントカレンダー最終回

学生から社会人、資質の変化は見られるのか 7年ぶりのストレングスファインダーを受けてみた

技術もお笑いも見習い中の新卒2年目エンジニアが語る フォルシアの顧客チーム

圧縮アルゴリズムZstandardを導入しバッチ処理時間を短縮 データ鮮度を改善した話

昭和のAIスキルでどこまで立ち向かえるのか　対戦型ゲームAIコンテスト奮闘記

「CTFを作ってみた」　アドベントカレンダー最終回

学生から社会人、資質の変化は見られるのか　7年ぶりのストレングスファインダーを受けてみた

技術もお笑いも見習い中の新卒2年目エンジニアが語る　フォルシアの顧客チーム

圧縮アルゴリズムZstandardを導入しバッチ処理時間を短縮　データ鮮度を改善した話