緑コーダーが頑張ってDPを使ったナップサック問題に挑戦してみた
技術本部の高橋です。これまで何度も解いてみようと思っては跳ね返され続けたこのDP、いわゆるナップサック問題に、緑コーダーの私が改めて挑戦してみました。
緑コーダーとは、Atcoderでレーティングが800~1199の人です。ちょっと競プロやってますというレベルで、AtCoderのC問題は解けるけど、D問題が解けないくらいの人だろうと自分では考えています。
すでに、動的計画法 / ナップサック問題の解説は多くありますが、この記事が少しでも私と同じような人の役に立てば幸いです。
DP?ナップサック問題?
DPとは
突然ですが、「DP」と言われて何のことだか分かりますか?
データプロセッサー、ダブルプレー...色々なものの略称として使われるようですが、フォルシアでは、主に次の3つの意味で使われることが多いです。
- Dynamic Package(ダイナミックパッケージ)
旅行商品の一つ。飛行機や新幹線などの交通手段とホテルなどの宿泊施設を利用者が自由に組み合わせて旅行プランを作成できる。 - Dynamic Pricing(ダイナミックプライシング)
需要と供給の状況に応じて価格を変動させる仕組み。売上の向上と潜在需要の創出を実現し需給をコントロールする。 - Dynamic Programming(動的計画法)
「動的計画法」と呼ばれるアルゴリズムの一つ。問題を複数の部分問題に分割し、部分問題の計算結果を利用して全体の最適化をはかる。
今回ご紹介するのは、3つ目にご紹介したDynamic Programming(動的計画法)。
(01)ナップサック問題とは
DPを使って解く典型的な問題の一つです。初心者がまず詰まる問題で、例えが古いかもしれませんが、高校数学のベクトルのような存在だと自分は考えています。例に漏れず、私も自分で実装しようとすると手が止まってしまい、何度解説を見てもしっくりきませんでした。
DPを理解するために
典型的な01ナップサック問題の設定だと、なんだかわくわくしないので、今回は、予算1000円でサイゼリヤに行って、同じものを頼まずに摂取できる最大のカロリーを求めるという問題にしてみました。メニューは自分がサイゼリヤに行ったらよく食べるものをチョイスしました。
メニュー
やわらかチキンのサラダ,134,299,1.2
半熟卵とポークのサラダ,433,599,2.3
ほうれん草のソテー,80,189,1.0
フレッシュチーズとトマトのサラダ,169,299,1.1
プロシュート(パルマ産熟成生ハム),225,399,2.7
辛味チキン,333,299,2.3
チョリソー(辛味ソーセージ),380,399,2.5
マルゲリータピザ,568,399,2.5
パンチェッタのピザ,646,399,2.4
アラビアータ,591,399,3.7
ミートソースボロニア風,538,399,3.6
ミラノ風ドリア,519,299,2.7
半熟卵のミラノ風ドリア,609,368,2.9
柔らかチキンのチーズ焼き,549,499,2.0
ミルクジェラート,100,199,0.1
イタリアンプリン,216,249,0.1
※塩分はなにか広げられるかと思って入れてみましたが、今回はそこまで手が出なかったので全く使っていません。
まずは全探索から始めてみよう
とは言ったものの、正直この全探索を作るのはなかなか難しかったです。次の2つが特に難しかった点です。
- 再帰でやるということを思い浮かばなかったら出来ない気がする
2^(メニューの数)回for文を回して、bitでやるとかなのでしょうか...
- 再帰でやるとなっても、引数をどうするのか、どういう関数にするのかが難しい
- カロリーは引数として取らなくていいのか
- n品目まで食べたとき、なのか、n品目以降なのか
全探索は再帰を使うというイメージがあったので、色々見ながらなんとか作ってみました。
今回は、n=0から始めて、n+1品目以降のメニューだけで選んだときに得られるカロリーを返す関数として考えてみました。プログラムは以下のとおりです。
コード
# ファイルの読み込み
with open('menu.csv') as fi:
menu = fi.readlines()
for i in range(len(menu)):
menu[i] = menu[i].strip().split(",")
for j in range(1,3):
menu[i][j] = int(menu[i][j])
menu[i][3] = float(menu[i][3])
yosan = 1000
# n+1品目以降のメニューで得られる最大のカロリーを求める関数
# 1品目はmenu[0]なので日本語とずれている
def zentansaku(n,ryoukin):
# もう料理が残っていなければカロリーは得られない
if n == len(menu):
return 0
# menu[n]の料金が予算内であれば、menu[n]を食べた場合と食べなかった場合を確かめる
if ryoukin + menu[n][2] <= yosan:
taberu = zentansaku(n + 1, ryoukin + menu[n][2]) + menu[n][1] # [1]はカロリー [2]は料金
tabenai = zentansaku(n + 1, ryoukin)
if taberu >= tabenai:
return taberu
else:
return tabenai
else:
tabenai = zentansaku(n + 1, ryoukin)
return tabenai
print(zentansaku(0,0)) # 1品目から0円使った状態での最大のカロリーを求める
出力結果
1498
やりました、再帰を使っての全探索は出来ました。そのメニューを食べるか食べないかで、maxを使わずに、いちいち`taberu`, `tabenai`に代入したのは、それぞれの値が何を指すのか一旦整理してみようと思ったり、日本語に近づけてみようと思ったという意図があります。
続いて、この全探索を高速化するメモ化。これはかなり直感的な手法で、すぐに理解できたので実装してみました。おまけに、再帰関数がどのように自分を呼び出していくのか、プログラムのどこを辿っていくのかを見てみようと思って色々出力してみました。これ以下のコードではファイル読み込みの部分は省略します。
コード
# (ファイル読み込み部分は省略) yosan = 1000 # メモ用の配列 memo = [[-1 for i in range(yosan+1)] for j in range(len(menu)+1)] def zentansaku(n,ryoukin): indent = " " * (n + 1) # メモされてたらその値を利用する if memo[n][ryoukin] != -1: return memo[n][ryoukin] if n == len(menu) - 1: return 0 if ryoukin + menu[n][2] <= yosan: print(indent,"| 食べてみる",n,ryoukin,menu[n][2]) taberu = zentansaku(n + 1, ryoukin + menu[n][2]) + menu[n][1] print(indent,"| 食べない",n,ryoukin) tabenai = zentansaku(n + 1, ryoukin) if taberu >= tabenai: # メモに記録 memo[n][ryoukin] = taberu print(indent,"[b]",menu[n][0],"を食べよう! ret:",taberu," / ",n,ryoukin,menu[n][2]) return taberu else: print(indent,"[!]",menu[n][0],"を食べないほうがたくさん食べれるようだ... ret:",tabenai, " / ", n,ryoukin,menu[n][2]) # メモに記録 memo[n][ryoukin] = tabenai return tabenai else: print(indent,"| 食べられない(お金がない)",n,ryoukin) tabenai = zentansaku(n + 1, ryoukin) # メモに記録 memo[n][ryoukin] = tabenai print(indent,"[x] お金がないので",menu[n][0],"は食べられない...ret:",tabenai," / ",n,ryoukin,menu[n][2]) return tabenai print(zentansaku(0,0))
出力結果
| 食べてみる 0 0 299
| 食べてみる 1 299 599
| 食べられない(お金がない) 2 898
| 食べられない(お金がない) 3 898
| 食べられない(お金がない) 4 898
| 食べられない(お金がない) 5 898
| 食べられない(お金がない) 6 898
| 食べられない(お金がない) 7 898
| 食べられない(お金がない) 8 898
| 食べられない(お金がない) 9 898
| 食べられない(お金がない) 10 898
| 食べられない(お金がない) 11 898
| 食べられない(お金がない) 12 898
| 食べられない(お金がない) 13 898
| 食べられない(お金がない) 14 898
[x] お金がないので ミルクジェラート は食べられない...ret: 0 / 14 898 199
[x] お金がないので 柔らかチキンのチーズ焼き は食べられない...ret: 0 / 13 898 499
[x] お金がないので 半熟卵のミラノ風ドリア は食べられない...ret: 0 / 12 898 368
[x] お金がないので ミラノ風ドリア は食べられない...ret: 0 / 11 898 299
[x] お金がないので ミートソースボロニア風 は食べられない...ret: 0 / 10 898 399
[x] お金がないので アラビアータ は食べられない...ret: 0 / 9 898 399
[x] お金がないので パンチェッタのピザ は食べられない...ret: 0 / 8 898 399
[x] お金がないので マルゲリータピザ は食べられない...ret: 0 / 7 898 399
[x] お金がないので チョリソー(辛味ソーセージ) は食べられない...ret: 0 / 6 898 399
[x] お金がないので 辛味チキン は食べられない...ret: 0 / 5 898 299
[x] お金がないので プロシュート(パルマ産熟成生ハム) は食べられない...ret: 0 / 4 898 399
[x] お金がないので フレッシュチーズとトマトのサラダ は食べられない...ret: 0 / 3 898 299
[x] お金がないので ほうれん草のソテー は食べられない...ret: 0 / 2 898 189
| 食べない 1 299
| 食べてみる 2 299 189
| 食べてみる 3 488 299
| 食べられない(お金がない) 4 787
| 食べられない(お金がない) 5 787
| 食べられない(お金がない) 6 787
| 食べられない(お金がない) 7 787
--------------------(略)--------------------
[b] パンチェッタのピザ を食べよう! ret: 1355 / 8 0 399
[!] マルゲリータピザ を食べないほうがたくさん食べれるようだ... ret: 1355 / 7 0 399
[!] チョリソー(辛味ソーセージ) を食べないほうがたくさん食べれるようだ... ret: 1355 / 6 0 399
[b] 辛味チキン を食べよう! ret: 1498 / 5 0 299
[!] プロシュート(パルマ産熟成生ハム) を食べないほうがたくさん食べれるようだ... ret: 1498 / 4 0 399
[!] フレッシュチーズとトマトのサラダ を食べないほうがたくさん食べれるようだ... ret: 1498 / 3 0 299
[!] ほうれん草のソテー を食べないほうがたくさん食べれるようだ... ret: 1498 / 2 0 189
[!] 半熟卵とポークのサラダ を食べないほうがたくさん食べれるようだ... ret: 1498 / 1 0 599
[!] やわらかチキンのサラダ を食べないほうがたくさん食べれるようだ... ret: 1498 / 0 0 299
1498
やったー、ナップサック問題解けた!と思いましたが、今回の主目的はDPを理解することでした。正直全探索も色々見よう見まねで書いたのですが、慣れるまでは天下り的にとりあえずやってみて、まずは理解を深める。そのうえで落ち着いて考えて自分で納得できるようにしていこうと思いました。
ちゃんとDPで解いた
DPについて勉強した私が思うDPの肝
- ある状態が、その前の状態の組み合わせで表されるものであれば、その状態を漸化式にして表して、それをプログラムに落とし込めば、DPになる
- DPは再帰ではなくfor文を使って表を順番に埋めていくもの
コード
# (ファイル読み込み部分は省略)
yosan = 1000
# dp[i][j] = i番目までの品を使って j円使った時の 最大カロリー
# menuの添字と違ってややこしいのは、dp[0]を何も食べないときとするので、
# dp[i][j]のiと日本語のi番目が対応することである。
# くどいようであるが、i番目の品 = menu[i-1]である。
# ex: dp[3][500]は3つ目まで(=menuの0~2)の商品を使って、500円まで使える時の最大カロリーを指す
dp = [[-1 for i in range(yosan + 1)] for j in range(len(menu) + 1)]
for i in range(len(dp[0])):
# 初期条件 / 0番目の商品までを使う = 何も食べられない = 何円使っても0カロリー
dp[0][i] = 0
# menu[n]を使って、 price円使った時の最大カロリーを順番に求めていく
for n in range(len(menu)):
for price in range(yosan + 1):
# tabeta = n-1までのmenuと, price - menu[n][2]円の状態から、 menu[n]を食べた場合
# tabenai = n-1までのmenuと, price円の状態
if price - menu[n][2] >= 0:
tabeta = dp[n][price - menu[n][2]] + menu[n][1]
tabenai = dp[n][price]
if tabeta >= tabenai:
dp[n + 1][price] = tabeta
else:
dp[n + 1][price] = tabenai
# priceがそもそもmenu[n][2]よりも安かったら、menu[n]を食べるという選択肢はないので、1つ前のpriceをそのまま使うほかない
else:
dp[n + 1][price] = dp[n][price]
# 求める答えはlen(menu)番目までの商品を使い、yosan円まで使える時の最大カロリー。
print(dp[len(menu)][yosan])
# dpのテーブルを出力してみる
# 横にyosan個あると見づらいので、50円刻みで出力する
temp = []
for i in range(0,yosan + 1,50):
# :が書式指定を行うための記号(演算子?)、_が埋める文字、<が左埋め、数字が桁数
temp.append('{:_<4}'.format(i))
for a in dp:
temp = []
for i in range(0,len(a),50):
temp.append('{:>4}'.format(a[i])) # >は右埋め(^は中央寄せ)
print(" ".join(temp))
出力結果
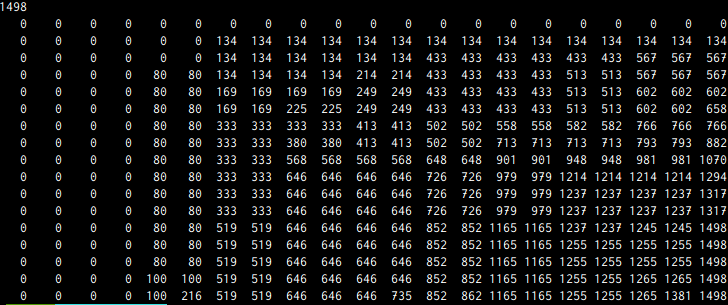
確かに上のメモ化再帰と同じ答えが出力されました!dpの表もなんだかそれらしくなっていて達成感があります。
当初の疑問点と今の理解
[Q1] なんでありえないような料金までfor文を回さないといけないのか。例えば50円と100円のメニューしかなければ、49円の状態とか存在しないのでは?
[A1] それはそうだけど、無駄になるだけで、実害はない。逆に、予算やカロリーが大きいと、大きい表を作らないといけなくなるので厳しい。その場合はもしかしたら工夫する必要があるかもしれない。
[Q2] dpの表をそうするというのはどうやったら思い浮かぶのか。
[A2] 慣れなのではないか。
[Q3] ある問題に対して表の作り方は一通りしかないのか。
[A3] 恐らくそんなことはない。何なら、この問題でも上記よりいい表の作り方がある可能性はある。制約に応じて表の持ち方を工夫するということは求められるのかもしれない。
感想
結局、ナップサック問題というのは、 dp[i][j] をどう作るかというゲームなのでは、ということと、どうやって漸化式を作るか、ということにかかっているのではないかということに、改めて気づきました。(それが思いついたら解けるんだろうし、それが思いつかないんですよと言いたい。)
しかしながら、今回、漸化式を思いついたらdpで問題が解けるようになったことは、一つ大きい収穫だと思っています。0-originと、日本語の~番目であったり、dpの添字とがなかなかうまく揃わなかったのが難しい/ミスが起きそうなポイントだなと思いました。前処理でうまく揃えて解くべきだったかもしれません。
あと、結局出力されたカロリーを取るには、何を食べればよいのかというのがわからないなと思っています。社内の競プロ強い人に聞いたら方法はあるようでしたが、今回は一旦ここまでとして、それについても考えていきたいなと思います。
今回は同じメニューを頼まないという縛りでしたが、同じメニューを頼むとしたらどうするのか、個数制限があったらどうなるのか、とか、「予算内でカロリー/円が最大になるのは」というのは一番カロリー/円の高いものを頼むだけになりそうなので、重複無しでm品以上頼むときの、という制約条件を付けるとどうなるのか、とか色々解いてみたくなりました。
自分には一生理解出来ないものとしてDPを扱っていましたが、今回親しみが持てました。現に、調べる中で最長共通部分列 という問題もDPを使うと知り、興味を持って調べました。問題を見たときはどうやってDPを使うのか思い浮かびませんでしたが、解説を見てハッとし、同時にその解説が分かるようになっていることに気づいて非常に嬉しくなりました。いつか、DPを使う問題を、これはDPで解く問題だ!と気づいて、AC取れることを夢見て、これからも競プロを頑張りたいと思います。
高橋紀光
技術第二部 エンジニア 2017年新卒入社。
宿泊横断検索サイトと社内のslackのスタンプ作成を主に担当。
たまに社内のカメラマンもやっている。



